题目内容
(本小题满分15分)
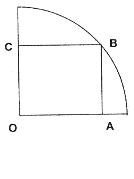
如图,在半径为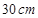 的
的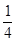 圆形(
圆形(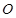 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料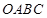 ,其中点
,其中点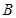 在圆上,点
在圆上,点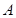 、
、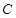 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮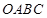 卷成一个以
卷成一个以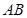 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长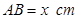 ,圆柱的体积为
,圆柱的体积为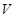
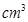 .
.
(1)写出体积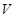 关于
关于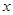 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;
(2)当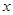 为何值时,才能使做出的圆柱形罐子体积
为何值时,才能使做出的圆柱形罐子体积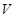 最大?最大体积是多少?
最大?最大体积是多少?
如图,在半径为
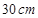 的
的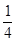 圆形(
圆形(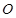 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料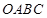 ,其中点
,其中点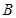 在圆上,点
在圆上,点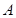 、
、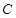 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮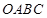 卷成一个以
卷成一个以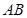 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长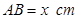 ,圆柱的体积为
,圆柱的体积为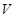
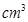 .
.
(1)写出体积
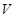 关于
关于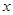 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;(2)当
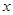 为何值时,才能使做出的圆柱形罐子体积
为何值时,才能使做出的圆柱形罐子体积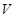 最大?最大体积是多少?
最大?最大体积是多少?(1) (2)当
(2)当 时,V有最大值
时,V有最大值
 (2)当
(2)当 时,V有最大值
时,V有最大值
试题分析:(1)连结OB,∵
 ,∴
,∴ ,
,设圆柱底面半径为
 ,则
,则 ,即
,即 ,
,所以
 其中
其中 。
。(2)由
 ,得
,得
因此
 在(0,
在(0, )上是增函数,在(
)上是增函数,在( ,30)上是减函数。
,30)上是减函数。所以当
 时,V有最大值
时,V有最大值 。
。点评:在求解函数应用题时注意实际限定条件对题目的影响

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
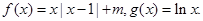 .
.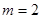 时,求函数
时,求函数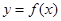 在
在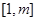 上的最大值;
上的最大值; ,若函数
,若函数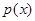 有零点,求
有零点,求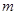 的取值范围.
的取值范围. 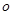 的函数关系式为:
的函数关系式为: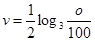 。若某条鱼想把游速提高1 m/s,它的耗氧量将增大到原来的a倍,则a=
。若某条鱼想把游速提高1 m/s,它的耗氧量将增大到原来的a倍,则a= 与每日生产产品件数
与每日生产产品件数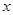 (
(
 )间的关系为
)间的关系为 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.
,每生产一件正品盈利4000元,每出现一件次品亏损2000元. (元)表示成日产量
(元)表示成日产量
 的零点个数为
的零点个数为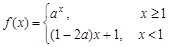 在
在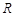 上单调递减,则实数
上单调递减,则实数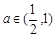 ;②若函数
;②若函数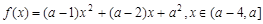 是偶函数,则实数
是偶函数,则实数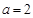 ;③若函数
;③若函数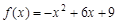 在区间
在区间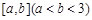 上有最大值9,最小值
上有最大值9,最小值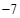 ,则
,则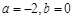 ;④
;④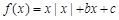 的图象关于点
的图象关于点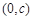 对称。其中正确的序号有 。
对称。其中正确的序号有 。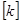 ,即
,即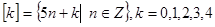 给出四个结论:
给出四个结论: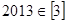 ,②
,②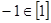 ,③
,③ ,④整数
,④整数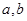 属于同一“类”,当且仅当是
属于同一“类”,当且仅当是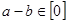 ,其中正确结论的个数是( )
,其中正确结论的个数是( )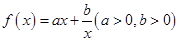 的单调性并给出证明。
的单调性并给出证明。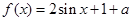 是一个奇函数.
是一个奇函数.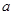 的值和
的值和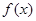 的值域;
的值域; >
> ,若
,若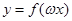 在区间
在区间 是增函数,求
是增函数,求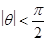 ,若对
,若对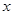 取一切实数,不等式
取一切实数,不等式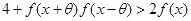 都成立,求
都成立,求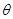 的取值范围.
的取值范围.