题目内容
(本题14分)
已知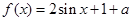 是一个奇函数.
是一个奇函数.
(1)求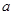 的值和
的值和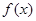 的值域;
的值域;
(2)设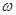 >
> ,若
,若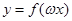 在区间
在区间 是增函数,求
是增函数,求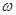 的取值范围
的取值范围
(3) 设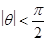 ,若对
,若对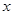 取一切实数,不等式
取一切实数,不等式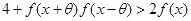 都成立,求
都成立,求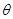 的取值范围.
的取值范围.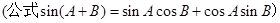
已知
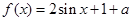 是一个奇函数.
是一个奇函数.(1)求
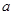 的值和
的值和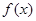 的值域;
的值域;(2)设
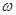 >
> ,若
,若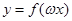 在区间
在区间 是增函数,求
是增函数,求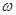 的取值范围
的取值范围(3) 设
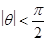 ,若对
,若对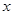 取一切实数,不等式
取一切实数,不等式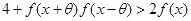 都成立,求
都成立,求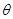 的取值范围.
的取值范围.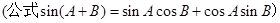
(1) .(2)
.(2) ;(3)
;(3)  .
.
 .(2)
.(2) ;(3)
;(3)  .
.试题分析:(1)根据
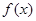 为奇函数,可得
为奇函数,可得 ,求得
,求得 ,进而求解值域。
,进而求解值域。(2) 首先把
 视为一个整体,求得得到函数的增区间,再利用
视为一个整体,求得得到函数的增区间,再利用
求得k值,进一步得到w的范围。
(3) 应用三角公式,将f(x)化简后, 得到
 ,只需
,只需 的最小值,转化成求二次函数的最小值问题。
的最小值,转化成求二次函数的最小值问题。解:(1)

 .
.∵
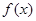 为奇函数,∴
为奇函数,∴ ,
, ,
,∴
 ,
, 的值域为
的值域为 .
.(2)
 当
当 时,
时,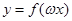 为增函数,∵
为增函数,∵
∴
 .
. ,
,∴
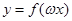 在区间
在区间 上是增函数
上是增函数依题意得
 ,
,∴
 ∴
∴ (
( ),
),∴
 得
得 (也可根据图象求解).
(也可根据图象求解).(3)





 .
.由原不等式得


 ,
,又∵
 .当且仅当
.当且仅当 取等号.
取等号.要使原不等式恒成立,须且只需
 ,∴
,∴ ,
,∵
 ,∴
,∴ .
.点评:解决该试题的关键是利用函数为奇函数,得到参数a的值,进而分析函数的单调性,熟练的掌握三角函数的单调区间很重要。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
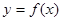 (
(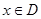 ,
,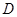 为此函数的定义域)同时满足下列两个条件:①函数
为此函数的定义域)同时满足下列两个条件:①函数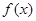
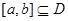 ,使函数
,使函数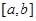 上的值域为
上的值域为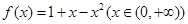 是否为闭函数?并说明理由;
是否为闭函数?并说明理由;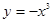 (
(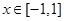 )为闭函数;
)为闭函数; 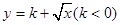 是闭函数,求实数
是闭函数,求实数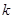 的取值范围.
的取值范围. 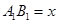 米,求公园ABCD所占面积S关于
米,求公园ABCD所占面积S关于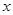 的函数
的函数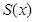 的解析式;
的解析式;
 分)已知函数
分)已知函数 .
. 与
与 ,
, 与
与 ;
; 与
与 有什么关系?并证明你的结论;
有什么关系?并证明你的结论; 的值 .
的值 .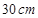 的
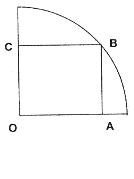
的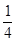 圆形(
圆形(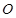 为圆心)铝皮上截取一块矩形材料
为圆心)铝皮上截取一块矩形材料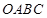 ,其中点
,其中点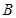 在圆上,点
在圆上,点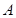 、
、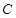 在两半径上,现将此矩形铝皮
在两半径上,现将此矩形铝皮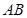 为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长
为母线的圆柱形罐子的侧面(不计剪裁和拼接损耗),设矩形的边长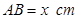 ,圆柱的体积为
,圆柱的体积为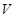
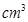 .
.
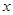 的函数关系式,并指出定义域;
的函数关系式,并指出定义域;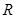 上的函数
上的函数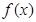 满足
满足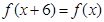 ,当
,当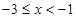 时,
时,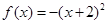 ,当
,当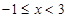 时,
时,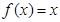 ,则
,则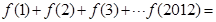
 ,则方程
,则方程 一定存在根的区间为( )
一定存在根的区间为( )


