题目内容
9.设集合P={(x,y)|x+y<4,x,y∈N*},则集合P的非空子集个数是7个.分析 分别对x取值1,2,3,求出满足条件的集合P中的元素,从而求出集合P的非空子集个数.
解答 解:当x=1时,y<3,又y∈N*,因此y=1或y=2;
当x=2时,y<2,又y∈N*,因此y=1;
当x=3时,y<1,又y∈N*,因此这样的y不存在.
综上所述,集合P中的元素有(1,1)、(1,2)、(2,1),
集合P的非空子集的个数是23-1=7,
故答案为:7.
点评 本题考查了集合的子集和真子集问题,是一道基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
20.点P是椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{9}$=1上一点,F1,F2分别是椭圆的左、右焦点,若|PF1||PF2|=12,则∠F1PF2的大小为( )
| A. | $\frac{5π}{6}$ | B. | $\frac{2π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
17.已知集合A={x|x2-2x>0},$B=\{x|\frac{x-2}{2x}≤1\}$,则A∩B=( )
| A. | [-2,0) | B. | (-2,0)∪(2,+∞) | C. | (-∞,-2]∪(2,+∞) | D. | [-1,0]∪[2,+∞) |
1.已知f(x)=$\left\{\begin{array}{l}{2^{1-x}},x≤1\\ 1-{log_2}^x,x>1\end{array}$则满足f(x)≤2的x取值范围是( )
| A. | [-1,2] | B. | [0,2] | C. | [1,+∞) | D. | [0,+∞) |
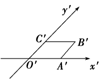 在直观图(如图所示)中,四边形O'A'B'C'为菱形且边长为2cm,则在xOy坐标系中,四边形OABC的面积为8cm2.
在直观图(如图所示)中,四边形O'A'B'C'为菱形且边长为2cm,则在xOy坐标系中,四边形OABC的面积为8cm2.