题目内容
16.已知向量$\overrightarrow{a}$=(sin θ,-2),$\overrightarrow{b}$=(cos θ,1),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则tan 2θ=$\frac{4}{3}$.分析 由$\overrightarrow{a}$∥$\overrightarrow{b}$,得到sin θ=-2cos θ,从而tan θ=-2,再由正切函数二倍角公式能求出tan 2θ的值.
解答 解:∵向量$\overrightarrow{a}$=(sin θ,-2),$\overrightarrow{b}$=(cos θ,1),$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴sin θ=-2cos θ,∴tan θ=-2,
故tan 2θ=$\frac{2tanθ}{1-tan2θ}$=$\frac{-4}{1-4}$=$\frac{4}{3}$.
故答案为:$\frac{4}{3}$.
点评 本题考查正切值的二倍角的求法,是基础题,解题时要认真审题,注意平面向坐标运算法则、向量平行的性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.在2L高产优质小麦种子中混入了一粒带白粉病的种子,从中随机取出10mL,则含有白粉病种子的概率是( )
| A. | $\frac{1}{20}$ | B. | $\frac{1}{50}$ | C. | $\frac{1}{100}$ | D. | $\frac{1}{200}$ |
8.已知直线l:x-$\sqrt{3}$y+6=0与圆x2+y2=12交于A,B两点,过A,B分别作l的垂线与x轴交于C,D两点,则|CD|=( )
| A. | $2\sqrt{3}$ | B. | 4 | C. | $4\sqrt{3}$ | D. | 6 |
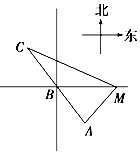 如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于2km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,则塔M到直路ABC的最短距离为$\frac{14+10\sqrt{3}}{13}$.
如图所示,已知A、B、C是一条直路上的三点,AB与BC各等于2km,从三点分别遥望塔M,在A处看见塔在北偏东45°方向,在B处看塔在正东方向,在点C处看见塔在南偏东60°方向,则塔M到直路ABC的最短距离为$\frac{14+10\sqrt{3}}{13}$.