题目内容
6.点P在边长为1的正方形ABCD内运动,则动点P到顶点A的距离|PA|≤1概率为( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | π |
分析 根据已知条件,求出满足条件的正方形ABCD的面积,以及动点P到定点A的距离|PA|≤1对应的平面区域面积,代入几何概型计算公式加以计算,可得所求概率.
解答 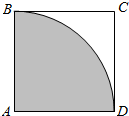 解:作出满足条件的正方形ABCD,如图所示.
解:作出满足条件的正方形ABCD,如图所示.
其中使得动点P到定点A的距离|PA|≤1的平面区域,是以A为圆心半径等于1的扇形ABD内部,如图中阴影所示.
∵正方形的面积S=1,扇形ABD的面积S′=$\frac{π}{4}$
∴动点P到定点A的距离|PA|≤1的概率P=$\frac{S′}{S}$=$\frac{π}{4}$.
故选:C.
点评 本题给出正方形ABCD内的动点P,求|PA|≤1的概率.着重考查了正方形与扇形的面积公式、几何概型计算公式等知识点,

练习册系列答案
 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案
相关题目
11.执行如图所示的程序框图,则输出的i值为( )
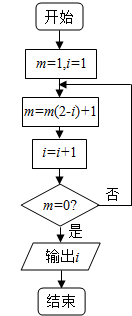

| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
15.已知集合A={x|x>1},B={x|(x+1)(x-2)<0},则A∪B=( )
| A. | {x|x>-1} | B. | {x|-1<x≤1} | C. | {x|-1<x<2} | D. | {x|1<x<2} |
16.已知数列{an}的前n项和为Sn,Sn=n2+1,则a5=( )
| A. | 7 | B. | 9 | C. | 11 | D. | 12 |