题目内容
14.已知等比数列{an}是递增数列,且${a_1}{a_{13}}+2{a_7}^2=4π$,则tan(a2a12)=$\sqrt{3}$.分析 由已知结合等比数列的性质求得${{a}_{7}}^{2}$,进一步求得tan(a2a12)的值.
解答 解:在等比数列{an}中,由${a_1}{a_{13}}+2{a_7}^2=4π$,得
$3{{a}_{7}}^{2}=4π$,即${{a}_{7}}^{2}=\frac{4π}{3}$.
∴tan(a2a12)=tan${{a}_{7}}^{2}=tan\frac{4π}{3}=tan\frac{π}{3}=\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 本题考查等比数列的性质,考查了三角函数值的求法,是基础的计算题.

练习册系列答案
相关题目
4.已知函数$f(x)=\left\{\begin{array}{l}x(x-1),x>0\\{log_3}(1-x),x≤0\end{array}\right.$,若f(m)=2,则实数m的值为( )
| A. | -1或2 | B. | -8或-1 | C. | -8或2 | D. | -8,-1或2 |
5.抛物线x2=4y的准线与y轴的交点的坐标为( )
| A. | $(0,-\frac{1}{2})$ | B. | (0,-1) | C. | (0,-2) | D. | (0,-4) |
19.已知函数f(x)=kx-1,其中实数k随机选自区间[-1,2].则对任意的x∈[-1,1],f(x)≤0的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
6.点P在边长为1的正方形ABCD内运动,则动点P到顶点A的距离|PA|≤1概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | π |
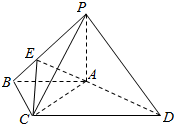 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=∠CAD=90°,点E在棱PB上,且PE=2EB,PA=AB=BC.
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,∠ABC=∠CAD=90°,点E在棱PB上,且PE=2EB,PA=AB=BC. 在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如下面的频率分布直方图所示.若该处高速公路规定正常行驶速度为90km/h~120km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有( )
在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如下面的频率分布直方图所示.若该处高速公路规定正常行驶速度为90km/h~120km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有( )