题目内容
11．命题“对任意的x∈R，x2-2x+1≥0”的否定是（ ）| A． | 不存在x0∈R，${x_0}^2-2{x_0}+1≥0$ | B． | 存在x0∈R，${x_0}^2-2{x_0}+1≤0$ | ||
| C． | 存在x0∈R，${x_0}^2-2{x_0}+1＜0$ | D． | 对任意的x∈R，x2-2x+1＜0 |
分析 特称命题的否定是全称命题，同时将命题的结论否定．
解答 解：根据全称命题的否定是特称命题可得命题“对任意的x∈R，x2-2x+1≥0”的否定是存在x0∈R，${x_0}^2-2{x_0}+1＜0$，
故选：C．
点评 本题考查特称命题的否定，解题的关键是熟练掌握特称命题的否定的书写规则，依据规律得到答案，要注意理解含有量词的命题的书写规则，特称命题的否定是全称命题，全称命题的否定是特称命题．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
6．已知条件p：k=$\sqrt{3}$；条件q：直线y=kx+2与圆x2+y2=1相切，则￢p是￢q的（ ）
| A． | 充分必要条件 | B． | 必要不充分条件 | ||
| C． | 充分不必要条件 | D． | 既不充分也不必要条件 |
3．如图所示，正方体ABCD-A′B′C′D′的棱长为1，O是平面A′B′C′D′的中心，则O到平面ABC′D′的距离是（ ）
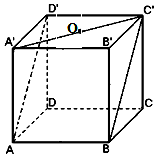
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{4}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
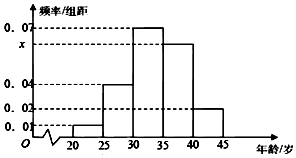为增强市民的节能环保意识，郑州市面向全市征召义务宣传志愿者，从符合条件的500名志愿者中随机抽取100名，其年龄频率分布直方图如图所示，其中年龄分组区是：[20，25]，[25，30]，[30，35]，[35，40]，[40，45]．