题目内容
已知扇形的周长为12cm,则该扇形面积的最大值为 cm2.
考点:扇形面积公式
专题:计算题,三角函数的求值
分析:由扇形的周长和面积公式都和半径和弧长有关,故可设出半径和弧长,表示出周长和面积公式,根据基本不等式做出面积的最大值即可.
解答:
解:设扇形半径为r,弧长为l,则周长为2r+l=12,面积为S=
lr,
因为12=2r+l≥2
,
所以rl≤18,
所以S≤9
故答案为:9.
| 1 |
| 2 |
因为12=2r+l≥2
| 2lr |
所以rl≤18,
所以S≤9
故答案为:9.
点评:本题考查扇形的周长和面积公式及利用基本不等式求最值,解题的关键是正确表示出扇形的面积,再利用基本不等式求解.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
已知sina+cosa=
,则sin2a=( )
| 1 |
| 3 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|

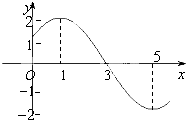 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<