题目内容
15.在△ABC中,内角A,B,C的对边长分别为a,b,c,若$\frac{a}{cosA}$=$\frac{b}{2cosB}$=$\frac{c}{3cosC}$,则sinB=$\frac{2\sqrt{5}}{5}$.分析 由$\frac{a}{cosA}$=$\frac{b}{2cosB}$=$\frac{c}{3cosC}$,利用正弦定理,可得tanA=$\frac{1}{2}$tanB=$\frac{1}{3}$tanC,再结合和角的正切公式,同角三角函数基本关系式,即可得出结论.
解答 解:∵$\frac{a}{cosA}$=$\frac{b}{2cosB}$=$\frac{c}{3cosC}$,
∴tanA=$\frac{1}{2}$tanB=$\frac{1}{3}$tanC,
∵tanB=tan(π-A-C)=-tan(A+C)=-$\frac{tanA+tanC}{1-tanAtanC}$=-$\frac{(\frac{1}{2}+\frac{3}{2})tanB}{1-\frac{1}{2}tanB×\frac{3}{2}tanB}$,
∴tan2B=4,
∴sinB=$\sqrt{1-\frac{1}{ta{n}^{2}B+1}}$=$\sqrt{1-\frac{1}{4+1}}$=$\frac{2\sqrt{5}}{5}$.
故答案为:$\frac{2\sqrt{5}}{5}$.
点评 本题考查正弦定理的运用,考查和角的正切公式,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
3.下列关于条件语句的叙述,正确的是( )
| A. | 条件语句中必须有if、else和end | |
| B. | 条件语句中可以没有end | |
| C. | 条件语句中可以没有else,但必须有end | |
| D. | 条件语句中可以没有else及没end |
10.下列函数中,y的最小值为2的是( )
| A. | y=x+$\frac{1}{x}$ | B. | y=x2+$\frac{1}{x^2}$ | C. | y=lgx+$\frac{1}{lgx}$ | D. | y=sinx+$\frac{1}{sinx}$ | ||||
| E. | y=x2+$\frac{1}{x^2}$ |
20.下列语句中的赋值语句是( )
| A. | x=x^3 | B. | 2=x | C. | x=y=2 | D. | x+y=z |
7.甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
(1)用茎叶图表示这两组数据;
(2)求两位学生预赛成绩的平均数和方差;
(3)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?请说明理由.
| 甲 | 82 | 81 | 79 | 78 | 95 | 88 | 93 | 84 |
| 乙 | 92 | 95 | 80 | 75 | 83 | 80 | 90 | 85 |
(2)求两位学生预赛成绩的平均数和方差;
(3)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为选派哪位学生参加合适?请说明理由.
4.做一个容积为4升的正方形底无盖水箱,要使得材料最省,则此水箱底面边长为( )
| A. | $\frac{1}{2}$分米 | B. | 1分米 | C. | 2分米 | D. | 4分米 |
5.函数y=$\frac{1}{x}$-2x的图象关于( )
| A. | y轴对称 | B. | x轴对称 | C. | 原点对称 | D. | y=x对称 |
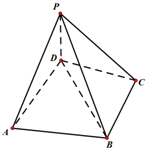 如图,四棱锥P-ABCD中,底面ABCD为四边形,△ABD是边长为2的正三角形,BC⊥CD,BC=CD,PD⊥AB,平面PBD⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为四边形,△ABD是边长为2的正三角形,BC⊥CD,BC=CD,PD⊥AB,平面PBD⊥平面ABCD.