题目内容
12.不等式sinx>a在x∈(-$\frac{π}{4}$,$\frac{π}{2}$)上恒成立,则a的取值范围为( )| A. | a>1 | B. | a≤1 | C. | a≤-$\frac{\sqrt{2}}{2}$ | D. | a$≤\frac{\sqrt{2}}{2}$ |
分析 设函数f(x)=sinx,x∈(-$\frac{π}{4}$,$\frac{π}{2}$),求出f(x)∈(-$\frac{\sqrt{2}}{2}$,1),即可得出结论.
解答 解:设函数f(x)=sinx,x∈(-$\frac{π}{4}$,$\frac{π}{2}$),
则f(x)∈(-$\frac{\sqrt{2}}{2}$,1),
∵不等式sinx>a在x∈(-$\frac{π}{4}$,$\frac{π}{2}$)上恒成立,
∴a≤-$\frac{\sqrt{2}}{2}$.
故选:C.
点评 本题结合不等式恒成立考查了三角函数的性质,求解最值,考查学生的计算能力,属于中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
2.函数$y=lg(\frac{2}{x+1}-1)$的图象关于( )
| A. | x轴成轴对称图形 | B. | y轴成轴对称图形 | ||
| C. | 原点成中心对称图形 | D. | 直线y=x成轴对称图形 |
16.已知复数z=a+(a2-1)i(a∈R,i为虚数单位),且z<0,则复数$\frac{i}{z}$=( )
| A. | i | B. | -i | C. | i或-i | D. | 1-a2-ai |
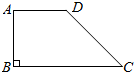 如图所示,已知AB是直角梯形ABCD与底边垂直的一腰,分别以AB,CD,DA为轴旋转,试说明所得几何体的结构特征.
如图所示,已知AB是直角梯形ABCD与底边垂直的一腰,分别以AB,CD,DA为轴旋转,试说明所得几何体的结构特征.