题目内容
已知函数f(x)=sin(π-x)sin(
-x)+cos2x.
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调区间.
| π |
| 2 |
(1)求函数f(x)的最小正周期;
(2)求函数f(x)的单调区间.
考点:二倍角的余弦,复合三角函数的单调性
专题:三角函数的求值
分析:(1)利用三角恒等变换化简函数的解析式为函数f(x)=
sin(2x+
)+
,由此可得函数的周期.
(2)令2kπ-
≤2x+
≤2kπ+
,求得x的范围,可得函数的增区间;令2kπ+
≤2x+
≤2kπ+
,求得x的范围,可得函数的增区间.
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
(2)令2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
解答:
解:(1)函数f(x)=sin(π-x)sin(
-x)+cos2x=sinxcosx+
=
sin2x+
cos2x+
=
sin(2x+
)+
,
故函数的周期为
=π.
(2)令2kπ-
≤2x+
≤2kπ+
,求得 kπ-
≤x≤kπ+
,故函数的增区间为[kπ-
,kπ+
],k∈z.
令2kπ+
≤2x+
≤2kπ+
,求得 kπ+
≤x≤kπ+
,故函数的增区间为[kπ+
,kπ+
],k∈z.
| π |
| 2 |
| 1+cos2x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 4 |
| 1 |
| 2 |
故函数的周期为
| 2π |
| 2 |
(2)令2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| 3π |
| 8 |
| π |
| 8 |
| 3π |
| 8 |
| π |
| 8 |
令2kπ+
| π |
| 2 |
| π |
| 4 |
| 3π |
| 2 |
| π |
| 8 |
| 5π |
| 8 |
| π |
| 8 |
| 5π |
| 8 |
点评:本题主要考查三角函数的恒等变换及化简求值,正弦函数的周期性和单调性,属于基础题.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
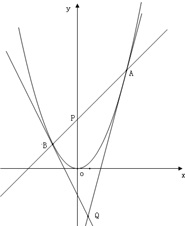 已知A、B为抛物线C:x2=2y上的两点,点P(0,t)(t>0)满足
已知A、B为抛物线C:x2=2y上的两点,点P(0,t)(t>0)满足