Question

14．关于x的方程lg（x-1）+lg（3-x）=lg（a-x），其中a是实常数．
（1）当a=2时，解上述方程
（2）根据a的不同取值，讨论上述方程的实数解的个数．

Answer 1

分析 （1）由对数的含义及运算法则，转化为二次方程的解，解出即可；（2）由对数的含义及运算法则，转化为二次方程的解得问题处理即可，注意定义域．

解答 解：（1）a=2时，lg（x-1）+lg（3-x）=lg（2-x），x∈（1，2），
故（x-1）（3-x）=2-x，整理得：x²-5x+5=0，
△=25-20=5＞0，
x=$\frac{5±\sqrt{5}}{2}$，∵x∈（1，2），
故x=$\frac{5-\sqrt{5}}{2}$；
（2）由题意x-1＞0且3-x＞0，所以1＜x＜3，
又lg（x-1）+lg（3-x）=lg（x-1）（3-x）=lg（a-x）
所以（x-1）（3-x）=a-x在1＜x＜3上有两个实根，
即判断x²-5x+a+3=0在（1，3）上个实根的个数．
所以a=-x²+5x-3，x∈（1，3），
令f（x）=-x²+5x-3，x∈（1，3），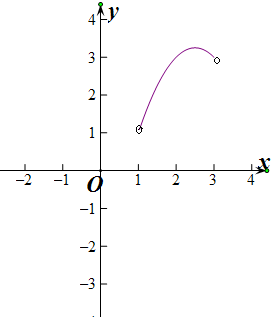

f（1）=1，f（3）=3，f（$\frac{5}{2}$）=$\frac{13}{4}$，
当1＜a≤3，或a=$\frac{13}{4}$时，方程有1个实根，
当3＜a＜$\frac{13}{4}$时，方程有2个实根，
当a＞$\frac{13}{4}$，a＜1时，方程无实根．

点评 本题考查二次方程实根分布问题、对数的运算法则，同时考查等价转化思想，属于中档题．