题目内容
10.设实数x,y满足不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{y≥x-1}\\{y≤5-2x}\end{array}\right.$,(2,1)是目标函数z=-ax+y取最大值的唯一最优解,则实数a的取值范围是( )| A. | (0,1) | B. | (0,1] | C. | (-∞,-2) | D. | (-∞,-2] |
分析 作出不等式组对应的平面区域,利用目标函数的几何意义,利用2,1)是目标函数z=-ax+y取最大值的唯一最优解,得到直线y=ax+z斜率的变化,从而求出a的取值范围.
解答 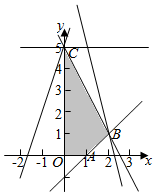 解:作出不等式组对应的平面区域如图:(阴影部分ABC).
解:作出不等式组对应的平面区域如图:(阴影部分ABC).
则A(1,0),B(2,1),C(0,5)
由z=y-ax得y=ax+z,即直线的截距最大,z也最大.
平移直线y=ax+z,则直线的截距最大时,z也最大,
当a=0时,y=z在C的截距最大,此时不满足条件,
当a>0时,直线y=ax+z,在C处的截距最大,此时不满足条件.
当a<0时,直线y=ax+z,要使,(2,1)是目标函数z=-ax+y取最大值的唯一最优解,
则y=ax+z在B处的截距最大,此时满足目标函数的斜率a小于直线BC的斜率-2,
即a<-2,
故选:C.
点评 本题主要考查线性规划的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
1.2位男生和3位女生共5位同学站成一排,则3位女生中有且只有两位女生相邻的概率是( )
| A. | $\frac{3}{10}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{1}{5}$ |
15.已知x、y满足不等式组$\left\{\begin{array}{l}x≥0\\ x-y≤0\\ 4x+3y≤14\end{array}$,设(x+2)2+(y+1)2的最小值为ω,则函数f(t)=sin(ωt+$\frac{π}{6}$)的最小正周期为( )
| A. | $\frac{π}{2}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{5}$ |
2.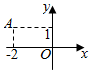 如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
 如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )
如图,在复平面内,表示复数z的点为A,则复数$\frac{z}{1-2i}$对应的点在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |