题目内容
20．设函数f（x）=ekx-1（k∈R）．（Ⅰ）当k=1时，求曲线y=f（x）在点（0，f（0））处的切线方程；
（Ⅱ）设函数F（x）=f（x）+x2-kx，证明：当x∈（0，+∞）时，F（x）＞0．
分析 （Ⅰ）求出f（x）的导数，可得切线的斜率和切点，由点斜式方程即可得到所求；
（Ⅱ）求出F'（x），令g（x）=kekx+2x-k，求得导数，判断单调性，即可得证．
解答 （本小题满分13分）
解：（Ⅰ）f′（x）=ex，…．（1分）
将x=0分别代入f（x）和f′（x）得，f′（0）=1，f（0）=0…．（3分）
所以曲线在点（0，f（0））处的切线方程为：y=x．…．（4分）
（Ⅱ）证明：F'（x）=kekx+2x-k…．（6分）
令g（x）=kekx+2x-k，则g'（x）=k2ekx+2…．（8分）
∵ekx＞0，k2≥0，∴g'（x）=k2ekx+2＞0…．（10分）
∴g（x）在（0，+∞）上单调递增，
∴g（x）＞g（0）=0即F'（x）＞0，…．（11分）
∴F（x）在（0，+∞）上单调递增，
∴F（x）＞F（0）=0…．（13分）
点评 本题考查导数的运用：求切线方程和单调区间，考查不等式的证明，注意运用单调性，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
10．
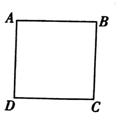如图，正方形ABCD边长为1，从某时刻起，将线段AB，BC，CD，DA分别绕点A，B，C，D顺时针旋转相同角度α（0＜α＜$\frac{π}{2}$），若旋转后的四条线段所围成的封闭图形面积为$\frac{1}{2}$，则α=（ ）
如图，正方形ABCD边长为1，从某时刻起，将线段AB，BC，CD，DA分别绕点A，B，C，D顺时针旋转相同角度α（0＜α＜$\frac{π}{2}$），若旋转后的四条线段所围成的封闭图形面积为$\frac{1}{2}$，则α=（ ）| A． | $\frac{π}{12}$或$\frac{5π}{12}$ | B． | $\frac{π}{12}$或$\frac{π}{3}$ | C． | $\frac{π}{6}$或$\frac{5π}{12}$ | D． | $\frac{π}{6}$或$\frac{π}{3}$ |
11．已知椭圆C：$\frac{{x}^{2}}{4}$+y2=1的左顶点为A，右顶点为B，点P是椭圆C上位于x轴上方的动点，直线AP，BP与直线y=3分别交于G，H两点，则线段GH的长度的最小值是（ ）
| A． | 5 | B． | 6 | C． | 7 | D． | 8 |
5．
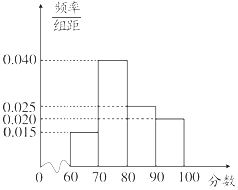2016年年底，某商业集团根据相关评分标准，对所属20家商业连锁店进行了年度考核评估，并依据考核评估得分（最低分60分，最高分100分）将这些连锁店分别评定为A，B，C，D四个类型，其考核评估标准如表：
考核评估后，对各连锁店的评估分数进行统计分析，得其频率分布直方图如下：
（Ⅰ）评分类型为A的商业连锁店有多少家；
（Ⅱ）现从评分类型为A，D的所有商业连锁店中随机抽取两家做分析，求这两家来自同一评分类型的概率．
2016年年底，某商业集团根据相关评分标准，对所属20家商业连锁店进行了年度考核评估，并依据考核评估得分（最低分60分，最高分100分）将这些连锁店分别评定为A，B，C，D四个类型，其考核评估标准如表：| 评估得分 | [60，70） | [70，80） | [80，90） | [90，100] |
| 评分类型 | D | C | B | A |
（Ⅰ）评分类型为A的商业连锁店有多少家；
（Ⅱ）现从评分类型为A，D的所有商业连锁店中随机抽取两家做分析，求这两家来自同一评分类型的概率．
10．己知函数y=f（x）-2x是偶函数，且f（1）=2，则f（-1）=（ ）
| A． | 2 | B． | -2 | C． | 0 | D． | 1 |