题目内容
6.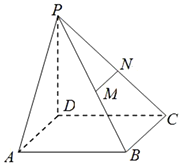 如图,已知四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.
如图,已知四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.(1)证明:MN∥平面PAD;
(2)若PB与平面ABCD所成的角为45°,求三棱锥C-BDN的体积V.
分析 (1)由MN∥BC∥AD即可得出MN∥AD,从而得出结论;
(2)连接BD,由PD=BD=2$\sqrt{2}$得出N到平面ABCD的距离为h=$\sqrt{2}$,则VC-BDN=VN-BCD=$\frac{1}{3}{S}_{△BCD}•h$.
解答  证明:(1)∵M,N是PB,PC的中点,
证明:(1)∵M,N是PB,PC的中点,
∴MN∥BC,又BC∥AD,
∴MN∥AD,又MN?平面PAD,AD?平面PAD,
∴MN∥平面PAD.
(2)连接BD,则BD=2$\sqrt{2}$,
∵PD⊥底面ABCD,
∴∠PBD为PB与平面ABCD所成的角,
∴∠PBD=45°,
∴PD=BD=2$\sqrt{2}$,
∵N为PC的中点,
∴N到平面ABCD的距离h=$\frac{1}{2}$PD=$\sqrt{2}$,
∴VC-BDN=VN-BCD=$\frac{1}{3}{S}_{△BCD}•h$=$\frac{1}{3}×\frac{1}{2}×2×2×\sqrt{2}$=$\frac{2\sqrt{2}}{3}$.
点评 本题考查了线面平行的判定定理,棱锥的体积计算,属于中档题.

练习册系列答案
相关题目
1.实数x,y满足$\left\{\begin{array}{l}x-y≥0\\ x+y≤1\\ y≥0\end{array}\right.$,则z=2x+y最大值为( )
| A. | 0 | B. | 1 | C. | 2 | D. | $\frac{3}{2}$ |
15.下列两个变量中,具有相关关系的是( )
| A. | 正方体的体积棱长 | B. | 匀速行驶的汽车的行驶距离与时间 | ||
| C. | 人的身高与体重 | D. | 人的身高与视力 |
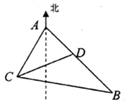 如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,则AC=24km.
如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,则AC=24km.