题目内容
18.已知函数f(x)=lnx-x.(1)求函数f(x)的单调区间;
(2)若方程f(x)=m(m<-2)有两个相异实根x1,x2,且x1<x2,证明:x1•x22<2.
分析 (1)确定函数的定义域,求导数,即可求函数f(x)的单调区间;
(2)证明x2>2,构造g(x)=lnx-x-m,证明g(x)在(0,1)上单调递增,即可证明结论.
解答 解:(1)f(x)=lnx-x的定义域为(0,+∞) …(1分)
令f′(x)<0得x>1,令f′(x)>0得0<x<1
所以函数f(x)=lnx-x的单调减区间是(1,+∞),单调递增区间(0,1)…(3分) …(4分)
(2)由(1)可设f(x)=m(m<-2)有两个相异实根x1,x2,满足lnx-x-m=0
且0<x1<1,x2>1,lnx1-x1-m=lnx2-x2-m=0 …(5分)
由题意可知lnx2-x2=m<-2<ln2-2 …(6分)
又由(1)可知f(x)=lnx-x在(1,+∞)递减
故x2>2 …(7分)
令g(x)=lnx-x-m
g(x1)-g($\frac{2}{{{x}_{2}}^{2}}$)=-x2+$\frac{2}{{{x}_{2}}^{2}}$+3lnx2-ln2 …(8分)
令h(t)=$-t+\frac{2}{{t}^{2}}$+3lnt-ln2(t>2),
则h′(t)=-$\frac{(t-2)^{2}(t+1)}{{t}^{3}}$.
当t>2时,h′(t)<0,h(t)是减函数,所以h(t)<h(2)=2ln2-$\frac{3}{2}$<0.…(9分)
所以当x2>2 时,g(x1)-g($\frac{2}{{{x}_{2}}^{2}}$)<0,即g(x1)<g($\frac{2}{{{x}_{2}}^{2}}$) …(10分)
因为g(x)在(0,1)上单调递增,
所以x1<$\frac{2}{{{x}_{2}}^{2}}$,故x1•x22<2. …(11分)
综上所述:x1•x22<2 …(12分)
点评 本题考查导数知识的运用,考查函数的单调性,考查不等式的证明,正确构造函数是关键.

| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
| A. | $\frac{20}{243}$ | B. | $\frac{8}{243}$ | C. | $\frac{4}{729}$ | D. | $\frac{4}{27}$ |
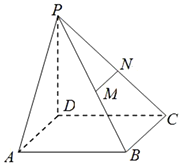 如图,已知四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.
如图,已知四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.