题目内容
14.已知α∥β,直线AB分别交于A,B,直线CD分别交α,β于C,D,AB∩CD=S,AS=4,BS=6,CD=5,则SC=10或 2.分析 作出图形,利用平面与平面平行推出直线与直线平行,通过相似列出比例关系,求解即可.
解答 解: 解:如图,α∥β,直线AB分别交α,β于A,B,直线CD分别交α,β于C,D,AB与CD相交于α,β同侧S,且AS=4,BS=10,CD=9,可知BD∥AC,
解:如图,α∥β,直线AB分别交α,β于A,B,直线CD分别交α,β于C,D,AB与CD相交于α,β同侧S,且AS=4,BS=10,CD=9,可知BD∥AC,
△SAC∽△SBD,
∴$\frac{SA}{SB}=\frac{SC}{SD}$,即$\frac{4}{6}=\frac{SC}{5+SC}$,
∴SC=10.
如图(2),由α∥β知AC∥BD,
△SAC∽△SBD,
∴$\frac{SA}{SB}=\frac{SC}{SD}$,即$\frac{4}{6}=\frac{SC}{5-SC}$,
∴SC=2.
故答案为:10或2.
点评 本题考查平面与平面平行的性质,相似三角形的性质,容易疏忽两种类型之一,是基础题,

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
5.等差数列{an}中,公差d=2,a1+a3+a5+…+a29=18,则a2+a4+a6+…+a30=( )
| A. | 20 | B. | 36 | C. | 48 | D. | 52 |
9.在△ABC中,A=45°,B=60°,a=$\sqrt{2}$,则b=( )
| A. | $\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
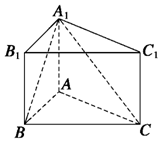 如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°.
如图,在直三棱柱ABC-A1B1C1中,AB=1,AC=AA1=$\sqrt{3}$,∠ABC=60°. 如图,菱形ABCD的边长为2,△BCD为正三角形,现将△BCD沿BD向上折起,折起后的点C记为C′,且CC′=$\sqrt{3}$,连接CC′,E为CC′的中点.
如图,菱形ABCD的边长为2,△BCD为正三角形,现将△BCD沿BD向上折起,折起后的点C记为C′,且CC′=$\sqrt{3}$,连接CC′,E为CC′的中点.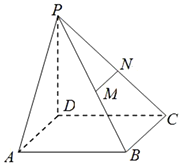 如图,已知四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.
如图,已知四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.