题目内容
16.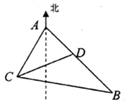 如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,则AC=24km.
如图,某观测站C在城A的南偏西20°的方向,从城A出发有一条走向为南偏东40°的公路,在C处观测到距离C处31km的公路上的B处有一辆汽车正沿公路向A城驶去,行驶了20km后到达D处,测得C,D两处的距离为21km,则AC=24km.
分析 根据题意可知CD,BC,BD在△BCD中,由余弦定理求得cos∠BDC,在△ACD中,由正弦定理求得AC.
解答 解:在△BCD中,CD=21,BD=20,BC=31,由余弦定理得cos∠BDC=$\frac{2{1}^{2}+2{0}^{2}-3{1}^{2}}{2×21×20}$=-$\frac{1}{7}$,
所以sin∠BDC=$\frac{4\sqrt{3}}{7}$.
在△ACD中,CD=21,∠CAD=20°+40°=60°,由正弦定理得AC=$\frac{21×\frac{4\sqrt{3}}{7}}{\frac{\sqrt{3}}{2}}$=24km.
故答案为:24km.
点评 本题主要考查了解三角形的实际应用.解题的关键是利用正弦定理,利用边和角的关系求得答案.

练习册系列答案
相关题目
11.已知集合A={1,2,3},集合B={4,5,6},映射f:A→B且满足1的象是4,则这样的映射有( )
| A. | 2个 | B. | 4个 | C. | 8个 | D. | 9个 |
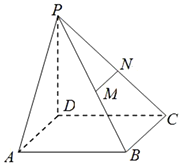 如图,已知四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.
如图,已知四棱锥P-ABCD中,PD⊥底面ABCD,且底面ABCD是边长为2的正方形,M、N分别为PB、PC的中点.