题目内容
14.已知一个几何体的三视图如图所示,则该几何体的体积为( )
| A. | 12π | B. | 8π | C. | $\frac{8π}{3}$ | D. | $\frac{20π}{3}$ |
分析 由几何体的三视图得该几何体的上半部分是一个圆锥,下半部分是一个圆柱,圆锥的高为2,底面半径是2,圆柱的高为4,底面半径为1,由此能求出这个几何体的体积.
解答 解:由几何体的三视图得该几何体的上半部分是一个圆锥,下半部分是一个圆柱,
圆锥的高为2,底面半径是2,圆柱的高为4,底面半径为1,
∴这个几何体的体积:
V=$π×{1}^{2}×4+\frac{1}{3}×π×{2}^{2}$×2=$\frac{20π}{3}$.
故选:D.
点评 本题考查几何体的体积的求法,是基础题,解题时要认真审题,注意三视图的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.已知α是第二象限角,且sin(π-α)=$\frac{3}{5}$,则sin2α的值为( )
| A. | -$\frac{24}{25}$ | B. | $\frac{24}{25}$ | C. | -$\frac{7}{25}$ | D. | -$\frac{24}{7}$ |
5.函数f(x)=$\frac{|cos(x-\frac{π}{2})|}{x}$-k在(0,+∞)上有两个不同的零点a,b(a<b),则下面结论正确的是( )
| A. | sina=acosb | B. | sinb=-bsina | C. | cosa=bsinb | D. | sina=-acosb |
19.以下命题正确的是( )
| A. | 经过空间中的三点,有且只有一个平面 | |
| B. | 空间中,如果两个角的两条边分别对应平行,那么这两个角相等 | |
| C. | 空间中,两条异面直线所成角的范围是(0,$\frac{π}{2}$] | |
| D. | 如果直线l平行于平面α内的无数条直线,则直线l平等于平面α |
3.设a=log30.3,b=20.3,c=0.32则( )
| A. | c>b>a | B. | c>a>b | C. | b>c>a | D. | b>a>c |
4.由直线y=2x及曲线y=4-2x2围成的封闭图形的面积为( )
| A. | 1 | B. | 3 | C. | 6 | D. | 9 |
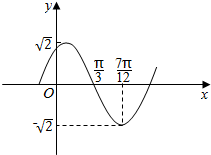 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数f(x)的解析式为f(x)=$\sqrt{2}$sin(2x+$\frac{π}{3}$),或f(x)=$\sqrt{2}$sin(2x-$\frac{2π}{3}$).
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则函数f(x)的解析式为f(x)=$\sqrt{2}$sin(2x+$\frac{π}{3}$),或f(x)=$\sqrt{2}$sin(2x-$\frac{2π}{3}$). 一个几何体的三视图如图所示,若其正视图、侧视图都是面积为$\frac{\sqrt{3}}{2}$,且一个角为60°的菱形,俯视图为正方形,则该几何体的体积为$\frac{\sqrt{3}}{3}$.
一个几何体的三视图如图所示,若其正视图、侧视图都是面积为$\frac{\sqrt{3}}{2}$,且一个角为60°的菱形,俯视图为正方形,则该几何体的体积为$\frac{\sqrt{3}}{3}$.