题目内容

如图，在边长为e（e为自然对数的底数）的正方形中随机撒一粒黄豆，则它落到阴影部分的概率为
 
．
考点：几何概型
专题：综合题,概率与统计
分析：利用定积分计算阴影部分的面积，利用几何概型的概率公式求出概率．
解答： 解：由题意，y=lnx与y=ex关于y=x对称，
∴阴影部分的面积为2
∫
1
0
（e-ex）dx=2（ex-ex）
|
1
0
=2，
∵边长为e（e为自然对数的底数）的正方形的面积为e2，
∴落到阴影部分的概率为
2
e2
．
故答案为：
2
e2
．
点评：本题考查几何概型，几何概型的概率的值是通过长度、面积、和体积的比值得到．
练习册系列答案
相关题目
若a＞b＞0，c＜d＜0，则一定有（　　）
A、
a
d
＞
b
c
B、
a
d
＜
b
c
C、
a
c
＞
b
d
D、
a
c
＜
b
d
从某企业生产的产品中抽取100件，测量这些产品的一项质量指标值，由测量结果得如下频数分布表：
质量指标值分组[75，85）[85，95）[95，105）[105，115）[115，125）
频数62638228
（1）在表格中作出这些数据的频率分布直方图；

（2）估计这种产品质量指标的平均数及方差（同一组中的数据用该组区间的中点值作代表）；
（3）根据以上抽样调查数据，能否认为该企业生产的这种产品符合“质量指标值不低于95的产品至少要占全部产品80%”的规定？
设F1，F2分别是椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，过点F1的直线交椭圆E于A，B两点，|AF1|=3|F1B|．
（Ⅰ）若|AB|=4，△ABF2的周长为16，求|AF2|；
（Ⅱ）若cos∠AF2B=
3
5
，求椭圆E的离心率．
定义域为R的偶函数f（x）满足对?x∈R，有f（x+2）=f（x）-f（1），且当x∈[2，3]时，f（x）=-2x2+12x-18，若函数y=f（x）-loga（|x|+1）在（0，+∞）上至少有三个零点，则a的取值范围是
 
．
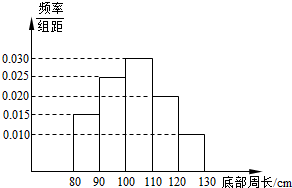为了了解一片经济林的生长情况，随机抽测了其中60株树木的底部周长（单位：cm），所得数据均在区间[80，130]上，其频率分布直方图如图所示，则在抽测的60株树木中，有
 
株树木的底部周长小于100cm．
如图，在平行四边形ABCD中，点E在AB上且EB=2AE，AC与DE交于点F，则
△CDF的周长
△AEF的周长
=
 
．
在平面直角坐标系中，O为原点，A（-1，0），B（0，
3
），C（3，0），动点D满足|
CD
|=1，则|
OA
+
OB
+
OD
|的最大值是
 
．
已知函数f（x）是定义在R上的奇函数，当x≥0时，f（x）=
1
2
（|x-a2|+|x-2a2|-3a2），若?x∈R，f（x-1）≤f（x），则实数a的取值范围为（　　）
A、[-
1
6
，
1
6
]
B、[-
6
6
，
6
6
]
C、[-
1
3
，
1
3
]
D、[-
3
3
，
3
3
]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网