题目内容
13．设集合U={1，2，3，4，5}，集合A={x∈Z|x2-5x+4＜0}，集合B={1，2}，则（∁UA）∩B=（ ）| A． | {1} | B． | {1，2} | C． | {1，3} | D． | {2，3} |
分析 解不等式x2-5x+4＜0即可求出集合A，然后进行补集、交集的运算即可．
解答 解：解x2-5x+4＜0得，1＜x＜4；
∴A={2，3}；
∴∁UA={1，4，5}，且B={1，2}；
∴（∁UA）∩B={1}．
故选：A．
点评 考查列举法、描述法表示集合的概念，以及交集和补集的运算．
练习册系列答案
备战中考寒假系列答案
相关题目
1．
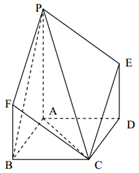如图，点P是菱形ABCD所在平面外一点，PA⊥平面ABCD，PA∥FB∥ED，∠ABC=60°，PA=AB=2BF=2DE．
（Ⅰ）求证：平面PAC⊥平面PCE；
（Ⅱ）求二面角B-PC-F的余弦值．
如图，点P是菱形ABCD所在平面外一点，PA⊥平面ABCD，PA∥FB∥ED，∠ABC=60°，PA=AB=2BF=2DE．（Ⅰ）求证：平面PAC⊥平面PCE；
（Ⅱ）求二面角B-PC-F的余弦值．
8．点P是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的右支上一点，其左，右焦点分别为F1，F2，直线PF1与以原点O为圆心，a为半径的圆相切于A点，线段PF1的垂直平分线恰好过点F2，则离心率的值为（ ）
| A． | $\frac{3}{2}$ | B． | $\frac{4}{3}$ | C． | $\frac{5}{3}$ | D． | $\frac{5}{4}$ |
18．如图是八位同学400米测试成绩的茎叶图（单位：秒），则（ ）
| A． | 平均数为64 | B． | 众数为7 | C． | 极差为17 | D． | 中位数为64.5 |
2．已知双曲线C1：x2-y2=a2（a＞0）关于直线y=x-2对称的曲线为C2，若直线2x+3y=6与C2相切，则实数a的值为（ ）
| A． | $\frac{{2\sqrt{5}}}{5}$ | B． | $\frac{8}{5}$ | C． | $\frac{4}{5}$ | D． | $\frac{{8\sqrt{5}}}{5}$ |
某市为了鼓励市民节约用水，实行“阶梯式”水价，将该市每户居民的月用水量划分为三档：月用水量不超过4吨的部分按2元/吨收费，超过4吨但不超过8吨的部分按4元/吨收费，超过8吨的部分按8元/吨收费．