题目内容
正方体ABCD-A1B1C1D1中，M，N分别是AA1和BB1的中点，G是BC上一点，使C1N⊥MG，则∠D1NG=______．
连接MN，
∵M，N分别是AA1和BB1的中点，
由正方体的几何特征可得MN∥C1D1，
在正方体ABCD-A1B1C1D1中，D1C1⊥平面B1C1CB
∵C1N?平面B1C1CB
∴D1C1⊥C1N
∴MN⊥C1N
又∵C1N⊥MG，MN∩MG=M，MD1，MG?平面MNG
∴C1N⊥平面MNG
又∵NG?平面MNG
∴C1N⊥NG
故∠D1NG=90°
故答案为：90°
∵M，N分别是AA1和BB1的中点，
由正方体的几何特征可得MN∥C1D1，
在正方体ABCD-A1B1C1D1中，D1C1⊥平面B1C1CB
∵C1N?平面B1C1CB
∴D1C1⊥C1N
∴MN⊥C1N
又∵C1N⊥MG，MN∩MG=M，MD1，MG?平面MNG
∴C1N⊥平面MNG
又∵NG?平面MNG
∴C1N⊥NG
故∠D1NG=90°
故答案为：90°
练习册系列答案
相关题目
是以
为半径的球
的小圆，若圆
和球
的比为
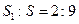，则圆心
＿＿＿＿＿。
垂直于矩形
所在的平面，
，
，
、
分别是
、
的中点。（1）求证：
平面
； 
平面
；
的大小. 
的棱上到异面直线AB，C
的距离相等的点的个数为( )
