题目内容
15.已知数列{an}满足an=3an-1+3n(n≥2,n∈N*),首项a1=3.(1)求数列{an}的通项公式;
(2)求数列{an}的前n项和Sn;
(3)数列{bn}满足bn=log3$\frac{a_n}{n}$,记数列{$\frac{1}{{{b_n}•{b_{n+1}}}}$}的前n项和为Tn,A是△ABC的内角,若sinAcosA>$\frac{{\sqrt{3}}}{4}{T_n}$对于任意n∈N*恒成立,求角A的取值范围.
分析 (1)通过在${a_n}-3{a_{n-1}}={3^n}$两边同时除以3n,进而可知数列$\left\{{\frac{a_n}{3^n}}\right\}$是首项为$\frac{a_1}{3}=1$、公差为1的等差数列,计算即得结论;
(2)通过(1),利用错位相减法计算即得结论;
(3)通过(1)计算可知${b_n}={log_3}{3^n}=n$,进而利用错位相减法计算可知Tn=1-$\frac{1}{n+1}$,利用Tn<1及二倍角公式化简可知$sin2A≥\frac{{\sqrt{3}}}{2}$,结合A∈(0,π)计算即得结论.
解答 解:(1)数列{an}满足${a_n}=3{a_{n-1}}+{3^n}$(n≥2,n∈N*),
∴${a_n}-3{a_{n-1}}={3^n}$,
又∵3n≠0,
∴$\frac{a_n}{3^n}-\frac{{a{\;}_{n-1}}}{{{3^{n-1}}}}=1$为常数,
∴数列$\left\{{\frac{a_n}{3^n}}\right\}$是首项为$\frac{a_1}{3}=1$、公差为1的等差数列,
∴$\frac{{a}_{n}}{{3}^{n}}$=n,∴${a_n}=n•{3^n}$(n∈N*);
(2)由(1)可知${S_n}=3+2•{3^2}+3•{3^3}+4•{3^4}+…+(n-1)•{3^{n-1}}+n•{3^n}$,
$3{S_n}={3^2}+2•{3^3}+3•{3^4}+4•{3^5}+…+(n-1)•{3^n}+n•{3^{n+1}}$,
两式错位相减,得:-2Sn=3+32+33+…+3n-n•3n+1
=$\frac{3(1-{3}^{n})}{1-3}$-n•3n+1
=-$\frac{3}{2}$-$\frac{2n-1}{2}$•3n+1,
∴Sn=$\frac{3}{4}$+$\frac{2n-1}{4}$•3n+1;
(3)由(1)可知${a_n}=n•{3^n}$,
∵数列{bn}满足${b_n}={log_3}\frac{a_n}{n}$,
∴${b_n}={log_3}{3^n}=n$,
∴$\frac{1}{{{b_n}{b_{n+1}}}}$=$\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}$,
∴${T_n}=(1-\frac{1}{2})+(\frac{1}{2}-\frac{1}{3})+(\frac{1}{3}-\frac{1}{4})+…+(\frac{1}{n}-\frac{1}{n+1})$=$1-\frac{1}{n+1}$,
又∵$sinAcosA=\frac{1}{2}sin2A>\frac{{\sqrt{3}}}{4}{T_n}$恒成立,且对于任意n∈N*,Tn<1成立,
∴$\frac{1}{2}sin2A≥\frac{{\sqrt{3}}}{4}$,即$sin2A≥\frac{{\sqrt{3}}}{2}$,
又A∈(0,π),即2A∈(0,2π),
∴$\frac{π}{3}≤2A≤\frac{2π}{3}$,即$A∈[{\frac{π}{6},\frac{π}{3}}]$.
点评 本题考查数列的通项及前n项和,考查错位相减法、裂项相消法,涉及三角函数等基础知识,对表达式的灵活变形是解决本题的关键,注意解题方法的积累,属于中档题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | (-1,$\frac{{{e^2}-1}}{2e-1}$) | B. | (1,+∞) | C. | ($\frac{{{e^2}-1}}{2e-1}$,2) | D. | ($\frac{{{e^2}-1}}{2e-1}$,+∞) |
| A. | 0.1 | B. | 0.2 | C. | 0.4 | D. | 0.8 |
| A. | $\sqrt{3}$ | B. | $\sqrt{7}$ | C. | $\sqrt{19}$ | D. | $\sqrt{23}$ |
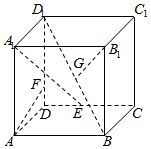 已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论:
已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论: