题目内容
5.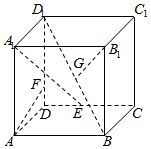 已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论:
已知正方体ABCD-A1B1C1D1,点E,F,G分别是线段DC,D1D和D1B上的动点,给出下列结论:①对于任意给定的点E,存在点F,使得AF⊥A1E;
②对于任意给定的点F,存在点E,使得AF⊥A1E;
③对于任意给定的点G,存在点F,使得AF⊥B1G;
④对于任意给定的点F,存在点G,使得AF⊥B1G.
其中正确结论的个数是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 根据直线与直线、直线与平面的位置关系,分别分析选项,利用排除法能得出结论
解答 解:因为DE⊥平面A1D,根据三垂线定理,
①对于任意给定的点E,A1E在平面A1D的射影为A1D,
所以存在点F,使得AF⊥A1D,所以AF⊥A1E;
②如果对于任意给定的点F,存在点E,使得AF⊥A1E;那么AF⊥A1D,又AD1⊥A1D,
得到过A有两条直线与A1D垂直,故②错误;
③只有AF垂直D1G在平面BCC1B1中的射影时,AF⊥B1G,
∴③正确;
④只有AF⊥平面A1CD1时,④才正确,
∵过A点作平面A1BD1的垂线与BB1无交点,
∴④错误.
故选:C.
点评 本题考查直线与直线、直线与平面的位置关系的判断,是中档题,解题时要注意空间思维能力的培养.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
20.已知函数f(x)的图象是由函数g(x)=cosx的图象经过如下变换得到:先将g(x)的图象向右平移$\frac{π}{3}$个单位长度,再将其图象上所有点的横坐标变为原来的一半,纵坐标不变,则函数f(x)的图象的一条对称轴方程为( )
| A. | x=$\frac{π}{6}$ | B. | x=$\frac{5π}{12}$ | C. | x=$\frac{π}{3}$ | D. | x=$\frac{7π}{12}$ |
14.已知i是虚数单位,复数z=$\frac{m}{1-i}$(m∈R),若|z|=$\int_0^π{(sinx-\frac{1}{π}})dx$,则m的值为( )
| A. | $±\sqrt{2}$ | B. | 0 | C. | 1 | D. | 2 |