题目内容
函数y=x2-4x+3，x∈[0，3]的值域为 ．
考点：二次函数在闭区间上的最值
专题：函数的性质及应用
分析：先配方，求出函数的对称轴，利用二次函数的单调性即可求出．
解答：
解：∵y=x2-4x+3=（x-2）2-1，函数的对称轴x=2∈[0，3]，
∴此函数在[0，3]上的最小值为：-1，最大值为：3，
∴函数f（x）的值域是[-1，3]．
∴此函数在[0，3]上的最小值为：-1，最大值为：3，
∴函数f（x）的值域是[-1，3]．
点评：熟练掌握二次函数的单调性是解题的关键．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
相关题目
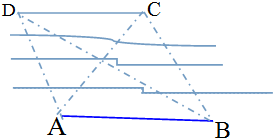如图所示，为了测量河对岸两个建筑物C，D两点之间的距离，在河岸这边选取点A，B，测得∠BAC=45°，∠DAC=75°，∠ABD=30°，∠DBC=45°，又已知AB=
如图，已知圆O1与圆O2交于A，B两点，圆O1上的点M处切线交圆O2于D，E两点，交直线AB于点C．若CM=2，CD=1，且∠DBE=30°，则圆O2的半径为