题目内容
已知两直线l1:ax-by+4=0和l2:(a-1)x+y+b=0.若l1∥l2且坐标原点到两直线的距离相等,求a、b的值.
考点:直线的一般式方程与直线的平行关系
专题:直线与圆
分析:根据l1∥l2可得:a+b(a-1)=0,…①;由l1,l2到两直线的距离相等,可得:
=
,…②,解方程组求出a,b并验证两条直线是否重合,可得答案.
| 4 | ||
|
| |b| | ||
|
解答:
解:∵直线l1:ax-by+4=0和l2:(a-1)x+y+b=0.
且l1∥l2,
∴a+b(a-1)=0,…①
又由l1,l2到两直线的距离相等,
∴
=
,…②
由①和②得
或
对于这两种情形,经检验知l1与l2都不重合.
∴
或
且l1∥l2,
∴a+b(a-1)=0,…①
又由l1,l2到两直线的距离相等,
∴
| 4 | ||
|
| |b| | ||
|
由①和②得
|
|
对于这两种情形,经检验知l1与l2都不重合.
∴
|
|
点评:本题考查的知识点是直线平行的充分条件,点到直线的距离公式,难度不大,熟练掌握相应公式是解答的关键.

练习册系列答案
相关题目
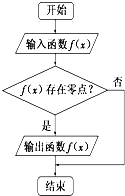 执行如图所示的程序框图,若输入如下四个函数:
执行如图所示的程序框图,若输入如下四个函数: