题目内容
6．已知在空间四边形ABCD中，$\overrightarrow{AB}=\vec a$，$\overrightarrow{BC}=\vec b$，$\overrightarrow{AD}=\vec c$，则$\overrightarrow{CD}$=（ ）| A． | $\vec a+\vec b-\vec c$ | B． | $\vec c-\vec a-\vec b$ | C． | $\vec c+\vec a-\vec b$ | D． | $\vec a+\vec b+\vec c$ |
分析 由空间四边形ABCD性质及向量加法法则得$\overrightarrow{CD}$=$\overrightarrow{BD}-\overrightarrow{BC}$=（$\overrightarrow{AD}-\overrightarrow{AB}$）-$\overrightarrow{BC}$，由此能求出结果．
解答 解：∵在空间四边形ABCD中，$\overrightarrow{AB}=\vec a$，$\overrightarrow{BC}=\vec b$，$\overrightarrow{AD}=\vec c$，
∴$\overrightarrow{CD}$=$\overrightarrow{BD}-\overrightarrow{BC}$=（$\overrightarrow{AD}-\overrightarrow{AB}$）-$\overrightarrow{BC}$
=（$\overrightarrow{c}-\overrightarrow{a}$）-$\overrightarrow{b}$
=$\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b}$．
故选：B．
点评 本题考查向量求法，是基础题，解题时要认真审题，注意向量加法法则的合理运用．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
16．诚信是立身之本，道德之基，某校学生会创设了“诚信水站”，既便于学生用水，又推进诚信教育，并用“$\frac{周实际回收水费}{周投入成本}$”表示每周“水站诚信度”，为了便于数据分析，以四周为一周期，如表为该水站连续十二周（共三个周期）的诚信数据统计：
（1）计算表中十二周“水站诚信度”的平均数$\overline{x}$；
（2）分别从表中每个周期的4个数据中随机抽取1个数据，设随机变量X表示取出的3个数据中“水站诚信度”超过91%的数据的个数，求随机变量X的分布列和期望；
（3）已知学生会分别在第一个周期的第四周末和第二个周期的第四周末各举行了一次“以诚信为本”的主题教育活动，根据已有数据，说明两次主题教育活动的宣传效果，并根据已有数据陈述理由．
| 第一周 | 第二周 | 第三周 | 第四周 | |
| 第一个周期 | 95% | 98% | 92% | 88% |
| 第二个周期 | 94% | 94% | 83% | 80% |
| 第三个周期 | 85% | 92% | 95% | 96% |
（2）分别从表中每个周期的4个数据中随机抽取1个数据，设随机变量X表示取出的3个数据中“水站诚信度”超过91%的数据的个数，求随机变量X的分布列和期望；
（3）已知学生会分别在第一个周期的第四周末和第二个周期的第四周末各举行了一次“以诚信为本”的主题教育活动，根据已有数据，说明两次主题教育活动的宣传效果，并根据已有数据陈述理由．
17．某四棱锥的三视图如图所示，则该四棱锥的体积是（ ）
| A． | 36 | B． | 24 | C． | 12 | D． | 6 |
14．已知命题p：直线$x+2y-\sqrt{2}=0$与直线$x+2y-6\sqrt{2}=0$之间的距离不大于1，命题q：椭圆2x2+27y2=54与双曲线9x2-16y2=144有相同的焦点，则下列命题为真命题的是（ ）
| A． | p∧（￢q） | B． | （￢p）∧q | C． | （￢p）∧（￢q） | D． | p∧q |
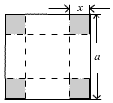如图所示，把一块边长是a的正方形铁片的各角切去大小相同的小正方形，再把它的边沿着虚线折转作成一个无盖方底的盒子，当盒子的容积最大时，切去的正方形的边长x为$\frac{a}{6}$．
15．sin390°等于（ ）
| A． | $\frac{1}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
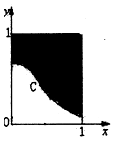在如图所示的正方形中随机投掷10000个点，则落入阴影部分（曲线C为正态分布N（0，1）的密度曲线）的点的个数的估计值为（ ）