题目内容
以下命题:
①已知函数f(x)=(a2-a-1)x
为幂函数,则a=-1;
②向量
=(-1,1)在向量
=(3,4)方向上的投影为
;
③函数f(x)=x2-2x的零点有2个;
④若扇形圆心角的弧度数为2,且扇形弧所对的弦长也是2,则这个扇形的面积为
.
所有真命题的序号是 .
①已知函数f(x)=(a2-a-1)x
| 1 |
| a-2 |
②向量
| a |
| b |
| 1 |
| 5 |
③函数f(x)=x2-2x的零点有2个;
④若扇形圆心角的弧度数为2,且扇形弧所对的弦长也是2,则这个扇形的面积为
| 1 |
| sin21 |
所有真命题的序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①已知函数f(x)=(a2-a-1)x
为幂函数,则
,解得即可;
②向量
=(-1,1)在向量
=(3,4)方向上的投影为
;
③当x>0时,f(2)=f(4)=0,当x≤0时,利用f(0)f(-1)<0,因此次函数在区间(-1,0)内有一个零点,即可判断出;
④若扇形圆心角的弧度数为2,且扇形弧所对的弦长也是2,则这个扇形的半径r=
,其面积=
×α•r2即可得出.
| 1 |
| a-2 |
|
②向量
| a |
| b |
| ||||
|
|
③当x>0时,f(2)=f(4)=0,当x≤0时,利用f(0)f(-1)<0,因此次函数在区间(-1,0)内有一个零点,即可判断出;
④若扇形圆心角的弧度数为2,且扇形弧所对的弦长也是2,则这个扇形的半径r=
| 1 |
| sin1 |
| 1 |
| 2 |
解答:
解:①已知函数f(x)=(a2-a-1)x
为幂函数,则
,解得a=-1,因此正确;
②向量
=(-1,1)在向量
=(3,4)方向上的投影为
=
=
,因此正确;
③当x>0时,f(2)=f(4)=0,当x≤0时,∵f(0)f(-1)<0,因此次函数在区间(-1,0)内有一个零点,故函数f(x)=x2-2x的零点有2个不正确;
④若扇形圆心角的弧度数为2,且扇形弧所对的弦长也是2,则这个扇形的半径r=
,其面积=
×α•r2=
×2×(
)2=
,因此正确.
所有真命题的序号是①②④.
故答案为:①②④.
| 1 |
| a-2 |
|
②向量
| a |
| b |
| ||||
|
|
| -3+4 | ||
|
| 1 |
| 5 |
③当x>0时,f(2)=f(4)=0,当x≤0时,∵f(0)f(-1)<0,因此次函数在区间(-1,0)内有一个零点,故函数f(x)=x2-2x的零点有2个不正确;
④若扇形圆心角的弧度数为2,且扇形弧所对的弦长也是2,则这个扇形的半径r=
| 1 |
| sin1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| sin1 |
| 1 |
| sin21 |
所有真命题的序号是①②④.
故答案为:①②④.
点评:本题综合考查了幂函数的定义、向量的投影、函数零点的个数、扇形的弧长公式及其面积计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
不等式2x-3<1的解集是( )
| A、(-∞,2] |
| B、(-∞,2) |
| C、(2,+∞) |
| D、[-∞,2) |
下列命题真命题是( )
①?p∈{正数},
为正数且
<p; ②不存在实数x,使x<4且x2+5x=24;
③?x∈R,使|x+1|≤1且x2>4; ④对实数x,若x2-6x-7=0,则x2-6x-7≥0.
①?p∈{正数},
| p |
| p |
③?x∈R,使|x+1|≤1且x2>4; ④对实数x,若x2-6x-7=0,则x2-6x-7≥0.
| A、① | B、④ | C、②③ | D、①④ |
设a,b是非零实数,若a<b,则下列不等式成立的是( )
| A、a2<b2 | ||||
B、
| ||||
| C、2a<2b | ||||
D、
|
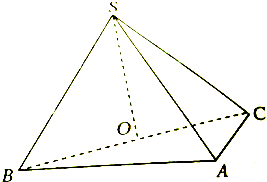 如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.
如图,在三棱锥S-ABC中,侧面SAB与侧面SAC均为等边三角形,∠BAC=90°,O为BC中点.