Question

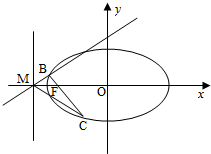如图，已知椭圆W：

x2

2m+10

+

y2

m2-2

=1的左焦点为F（m，0），过点M（-3，0）作一条斜率大于0的直线l与椭圆W交于不同的两点A、B，延长BF交椭圆W于点C．
（1）求椭圆W的离心率；
（2）若∠MAC=60°，求直线l的斜率．

Answer 1

考点：直线与圆锥曲线的关系

专题：圆锥曲线的定义、性质与方程

分析：对第（1）问，由左焦点F（m，0）知，焦点在x轴上，再根据a²=b²+c²，得m的等量关系，于是得m的值，从而解得a，c的值，再由e=

c

a

，可得离心率．
对第（2）问，设直线l的方程为y=kx+b，A，B的坐标分别为（x₁，k（x₁+3）），（x₂，k（x₂+3）），先证A关于x轴对称的点为C，即得△MAC为等腰三角形，由∠MAC=60°知，△MAC为正三角形，最后由k=tan∠AMO，得直线l的斜率．

解答： 解：（1）由左焦点F（m，0）知，焦点在x轴上，
且a²=2m+10＞0，b²=m²-2＞0，a²＞c²，a²＞b²，m＜0，
由a²=b²+c²，得2m+10=m²-2+m²，解得m=3（舍去），或m=-2，
从而a=

2m+10

=

6

，c=-m=2，
故椭圆W离心率e=

c

a

=

6

3

．

（2）设直线l的方程为y=kx+b，A（x₁，k（x₁+3）），B（x₂，k（x₂+3）），
则点A关于x轴对称的点为C′（x₁，k（x₁+3））．
下面证明B，F，C′三点共线：
只需证BF的斜率k_BF等于FC′的斜率k_FC′，
即证

k(x2+3)

x2+2

=

k(x1+3)

x1+2

，
化简、整理，得2x₁x₂+5（x₁+x₂）+12=0．…①
由

y=k(x+3) x2 6 + y2 2 =1

，消去y，整理得（3k²+1）x²+18k²x+27k²-6=0，
由韦达定理，得

x1+x2=- 18k2 3k2+1 x1x2= 27k2-6 3k2+1

，…②
将②代入①式左边，
得2•

27k2-6

3k2+1

-5•

18k2

3k2+1

+12=

-36k2-12+36k2+12

3k2+1

=0，即①式成立，
故B，F，C′三点共线，
∴C′与C重合，
∴AM=CM，
又∠MAC=60°，
∴△MAC为正三角形，
∴k=tan∠AMO=tan30°=

3

3

，
即直线l的斜率为

3

3

．

点评：本题考查了椭圆方程的求法，对直线与椭圆相交问题的处理方法等，常见思路是：
1、设直线方程及交点坐标；
2、联立直线与椭圆的方程消元，利用韦达定理进行整体代入，得到含参数的表达式或方程；
3、确定参数的值或范围．