题目内容
已知f(x)=x3+xsina,a∈(0,
),且f(kcosa)+f(1-k)≥0恒成立,求k的取值范围.
| π |
| 2 |
考点:函数恒成立问题
专题:计算题,函数的性质及应用,导数的综合应用,三角函数的图像与性质
分析:运用导数,判断单调性,由奇偶性的定义,确定奇函数,f(kcosa)+f(1-k)≥0恒成立即为f(kcosα)≥-f(1-k)=f(k-1),即有kcosα≥k-1即k≤
在α∈(0,
)恒成立,运用余弦函数的单调性,即可得到k的范围.
| 1 |
| 1-cosα |
| π |
| 2 |
解答:
解:f(x)=x3+xsina的导数f′(x)=3x2+sinα,
由于α∈(0,
),则sinα∈(0,1),
则f′(x)>0恒成立,即有f(x)在R上递增,
又f(-x)=-x3-xsinα=-f(x),即f(x)为奇函数,
f(kcosa)+f(1-k)≥0恒成立即为f(kcosα)≥-f(1-k)=f(k-1),
即有kcosα≥k-1即k≤
在α∈(0,
)恒成立,
由于cosα∈(0,1),则1-cosα∈(0,1),
∈(1,+∞),
即有k≤1.
即k的取值范围是(-∞,1].
由于α∈(0,
| π |
| 2 |
则f′(x)>0恒成立,即有f(x)在R上递增,
又f(-x)=-x3-xsinα=-f(x),即f(x)为奇函数,
f(kcosa)+f(1-k)≥0恒成立即为f(kcosα)≥-f(1-k)=f(k-1),
即有kcosα≥k-1即k≤
| 1 |
| 1-cosα |
| π |
| 2 |
由于cosα∈(0,1),则1-cosα∈(0,1),
| 1 |
| 1-cosα |
即有k≤1.
即k的取值范围是(-∞,1].
点评:本题考查函数的奇偶性和单调性的运用,考查运用导数判断函数的单调性,考查不等式恒成立问题,转化为求函数的范围,考查运算能力,属于中档题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
已知空间向量
=(2,-6,c),
=(1,-3,2),若
∥
,则c=( )
| a |
| b |
| a |
| b |
| A、4 | ||
| B、0 | ||
C、
| ||
D、
|
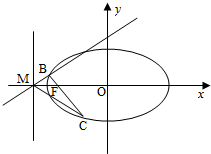 如图,已知椭圆W:
如图,已知椭圆W: