题目内容
12.定义在(1,+∞)上的函数f(x)满足:①对任意的x∈(1,+∞)恒有f(2x)=2f(x);②当x∈(1,2]时.f(x)=(2-x)3.若方程f(x)-k(x-1)=0恰有两个不同实根,则实数k的取值范围是( )| A. | [1,2) | B. | [$\frac{4}{3}$,2] | C. | ($\frac{4}{3}$,2) | D. | [$\frac{4}{3}$,2) |
分析 根据题中的条件分别求出函数f(x)在(1,8]上对应的解析式和图象,再结合函数的图象根据题意求出参数k的范围即可.
解答 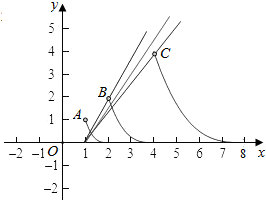 解:∵对任意的x∈(1,+∞)恒有f(2x)=2f(x);
解:∵对任意的x∈(1,+∞)恒有f(2x)=2f(x);
∴f(x)=2f($\frac{x}{2}$),
若x∈(2,4],则$\frac{x}{2}$∈(1,2],
此时f(x)=2f($\frac{x}{2}$)=2(2-$\frac{x}{2}$)3=$\frac{1}{4}$(4-x)3,
若x∈(4,8],则$\frac{x}{2}$∈(2,4],
此时f(x)=2f($\frac{x}{2}$)=2×$\frac{1}{4}$(4-$\frac{x}{2}$)3=$\frac{1}{2}$(4-$\frac{x}{2}$)3,
作出函数f(x)在(1,8]上的图象如图:B(2,2),C(4,4).
又kAB=$\frac{2-0}{2-1}$=2,kAC=$\frac{4-0}{4-1}$=$\frac{4}{3}$.
由题意得f(x)=k(x-1)的函数图象是过定点A(1,0)的直线,
如图所示红色的直线与线段AB相交即可(可以与B点重合但不能与A点重合)
分析图象知,当$\frac{4}{3}≤k<2$时f(x)=k(x-1)有两个不同的解.
故选:D.
点评 本题主要考查函数与方程的应用,解决此类问题的关键是熟悉求函数解析式的方法以及函数的图象与函数的性质,数形结合思想是高中数学的一个重要数学数学,是解决数学问题的必备的解题工具.

练习册系列答案
相关题目
3.函数y=2sinx(-π≤x≤π)的大致图象为( )
| A. |  | B. |  | C. |  | D. |  |
17.集合{x||x|≤3}用区间表示为( )
| A. | [-3,3] | B. | (-3,3) | C. | (-∞,3] | D. | [3,+∞) |
2.设A={x|$\frac{1}{x}$<0},S=R,则∁SA=( )
| A. | {x|$\frac{1}{x}$<0} | B. | {x|x<0} | C. | {x|x≤0} | D. | {x|x≥0} |
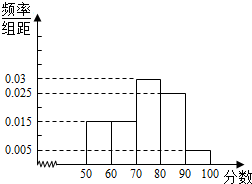 为更好地迎接江苏省学业水平测试,某校针对本届高二文科学生,进行了物理学科模拟测试,从参加测试的学生中抽出60名学生,对他们的物理成绩进行统计(注:学生成绩均为整数且满分为100分),并把其中成绩不低于50分的分成五段:[50,60),[60,70)…[90,100],画出如下部分频率分布直方图.请观察图形的相关信息,回答下列问题:
为更好地迎接江苏省学业水平测试,某校针对本届高二文科学生,进行了物理学科模拟测试,从参加测试的学生中抽出60名学生,对他们的物理成绩进行统计(注:学生成绩均为整数且满分为100分),并把其中成绩不低于50分的分成五段:[50,60),[60,70)…[90,100],画出如下部分频率分布直方图.请观察图形的相关信息,回答下列问题: