题目内容
11.过(2,2)点与双曲线x2$-\frac{y^2}{4}=1$有共同渐近线的双曲线方程为( )| A. | x2$-\frac{y^2}{4}=-1$ | B. | $\frac{x^2}{4}-{y^2}=1$ | C. | $\frac{x^2}{3}-\frac{y^2}{12}=1$ | D. | $\frac{y^2}{12}-\frac{x^2}{3}=1$ |
分析 要求的双曲线与双曲线x2-$\frac{{y}^{2}}{4}$=1有共同的渐近线,可设要求的双曲线的标准方程为:x2-$\frac{{y}^{2}}{4}$=λ.把点(2,2)代入可得λ,即可得出.
解答 解:∵要求的双曲线与双曲线x2-$\frac{{y}^{2}}{4}$=1有共同的渐近线,
∴可设要求的双曲线的标准方程为:x2-$\frac{{y}^{2}}{4}$=λ.
把点(2,2)代入可得:λ=4-1=3,
∴要求的双曲线的标准方程为:$\frac{{x}^{2}}{3}-\frac{{y}^{2}}{12}=1$.
故选C.
点评 本题考查了双曲线的标准方程及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19.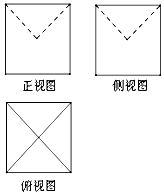 某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
 某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )
某几何体的三视图如图所示,图中的四边形都是边长为2的正方形,正视图和侧视图中的两条虚线都互相垂直且相等,则该几何体的体积是( )| A. | $8-\frac{π}{3}$ | B. | $8-\frac{π}{6}$ | C. | $\frac{20}{3}$ | D. | $\frac{16}{3}$ |
3.函数$f(x)={x^{\frac{1}{2}}}-2+{log_2}x$的零点所在区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,+∞) |
2.函数y=($\frac{1}{2}$)${\;}^{{x}^{2}}$+4x的值域为( )
| A. | [0,16] | B. | (0,16] | C. | (16,+∞) | D. | [16,+∞) |

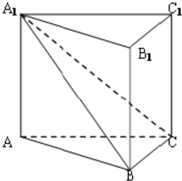 如图,在直三棱柱ABC-A1B1C1中,平面A1BC丄侧面A1AB B1,且 AA1=AB=2.
如图,在直三棱柱ABC-A1B1C1中,平面A1BC丄侧面A1AB B1,且 AA1=AB=2.