题目内容
在平面直角坐标系中,已知点A(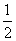 ,0),向量e=(0,1),点B为直线x=-
,0),向量e=(0,1),点B为直线x=-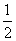 上的动点,点C满足
上的动点,点C满足 ,点M满足
,点M满足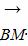 ·e=0,
·e=0,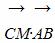 =0.
=0.
(1)试求动点M的轨迹E的方程;
(2)设点P是轨迹E上的动点,点R、N在y轴上,圆(x-1)2+y2=1内切于△PRN,求△PRN的面积的最小值.
(1)设M(x,y),B(-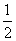 ,m),则
,m),则 =(x+
=(x+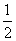 ,y-m),
,y-m),
∵ =(
=(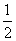 ,0)+(-
,0)+(-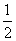 ,m)=(0,m),
,m)=(0,m),
∴C(0, ),
),
 所以动点M的轨迹E的方程为y2=2x.
所以动点M的轨迹E的方程为y2=2x.
(2)设P(x0,y0),R(0,b),N(0,c),且b>c,
∴lPR:y= +b,
+b,
即lPR:(y0-b)x-x0y+x0b=0,
由直线PR与圆相切得, =1,注意到x0>2,化简得(x0-2)b2+2y0b-x0=0,
=1,注意到x0>2,化简得(x0-2)b2+2y0b-x0=0,
同理得(x0-2)c2+2y0c-x0=0,
所以b,c是方程(x0-2)x2+2y0x-x0=0的两根,
所以|b-c|=
有S△PRN=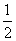 ·
· +4≥8,当x0=4时△PRN的面积的最小值为8.
+4≥8,当x0=4时△PRN的面积的最小值为8.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
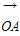 =(-1,t),
=(-1,t), =(2,2).若∠ABO=90°,则实数t的值为________.
=(2,2).若∠ABO=90°,则实数t的值为________. 与
与 满足|
满足| =
=

 的最小值为________.
的最小值为________.
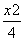 +y2=1的左、右焦点,过椭圆中心任作一直线与椭圆交于P、Q两点,当四边形PF1QF2面积最大时,
+y2=1的左、右焦点,过椭圆中心任作一直线与椭圆交于P、Q两点,当四边形PF1QF2面积最大时,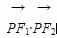 的值等于( )
的值等于( ) ,前n项和为Sn,则S2013=( )
,前n项和为Sn,则S2013=( )