题目内容
设F1、F2为椭圆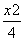
＋y2＝1的左、右焦点，过椭圆中心任作一直线与椭圆交于P、Q两点，当四边形PF1QF2面积最大时，
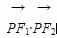的值等于( )
A．0 B．2 C．4 D．－2
D
[解析] 由题意得c＝
＝
，
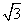又S四边形PF1QF2＝2S△PF1F2＝2×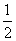
×F1F2·h (h为F1F2边上的高)，所以当h＝b＝1时，S四边形PF1QF2取最大值，此时∠F1PF2＝120°.
所以
·cos120°
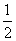＝2×2×(－)＝－2.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
( )
＝0，现将一粒黄豆随机撒在△ABC内，则黄豆落在△PBC内的概率是( )
B.
C.
的值为________．
，点M满足
·e＝0，
＝0.
) B．n(n－
)
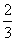) D．n(n－
)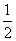