题目内容
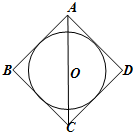如图，在正方形ABCD内作内切圆O，将正方形ABCD、圆O绕对角线AC旋转一周得到的两个旋转体的体积依次记为V1，V2，则V1：V2=（ ）A、2：
| ||
B、2
| ||
C、2：
| ||
D、
|
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：根据球的体积公式和圆锥的体积公式，分别求出V1，V2，可得答案．
解答：
解：设AC=BD=2，
则正方形ABCD旋转后得到两个底面半径为1，高为1的圆锥形成的组合体，
故V1=2×
×π=
，
圆O绕对角线AC旋转一周得到一个半径为
的球，
故V2=
（
）3=
，
故V1：V2=
：1，
故选：D
则正方形ABCD旋转后得到两个底面半径为1，高为1的圆锥形成的组合体，
故V1=2×
| 1 |
| 3 |
| 2π |
| 3 |
圆O绕对角线AC旋转一周得到一个半径为
| ||
| 2 |
故V2=
| 4π |
| 3 |
| ||
| 2 |
| ||
| 3 |
故V1：V2=
| 2 |
故选：D
点评：本题考查的知识点是旋转体，熟练掌握圆锥和球的体积公式，是解答的关键．
练习册系列答案
相关题目
设P为锐角△ABC的外心（三角形外接圆圆心），
=k（
+
）（k∈R）．若cos∠BAC=
，则k=（ ）
| AP |
| AB |
| AC |
| 2 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
下列几何体中不是旋转体的是（ ）
A、 |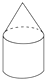
B、 |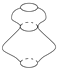
C、 |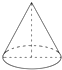
D、 |
“
=0”是“（x1，y1）、（x2，y2）、（x3，y3）三点共线”的（ ）
|
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
如果圆柱与圆锥的底面直径、高和球的直径相等，则体积比V圆柱：V圆锥：V球为（ ）
| A、3：1：2 | ||
| B、3：1：4 | ||
C、6：
| ||
| D、3：3：2 |