题目内容
6. 为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如右图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.
为了打好脱贫攻坚战,某贫困县农科院针对玉米种植情况进行调研,力争有效地改良玉米品种,为农民提供技术支援.现对已选出的一组玉米的茎高进行统计,获得茎叶图如右图(单位:厘米),设茎高大于或等于180厘米的玉米为高茎玉米,否则为矮茎玉米.(1)完成2×2列联表,并判断是否可以在犯错误概率不超过1%的前提下,认为抗倒伏与玉米矮茎有关?
(2)为了改良玉米品种,现采用分层抽样的方式从抗倒伏的玉米中抽出5株,再从这5株玉米中选取2株进行杂交实验,选取的植株均为矮茎的概率是多少?
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
分析 (1)计算K2,与临界值比较,即可得出结论;
(2)确定基本事件的个数,即可求出相应的概率.
解答 解:(1)根据统计数据做出2×2列联表如下:
| 抗倒伏 | 易倒伏 | 合计 | |
| 矮茎 | 15 | 4 | 19 |
| 高茎 | 10 | 16 | 26 |
| 合计 | 25 | 20 | 45 |
(2)分层抽样后,高茎玉米有2株,设为A,B,矮茎玉米有3株,设为a,b,c,从中取出2株的取法有AB,Aa,Ab,Ac,Ba,Bb,Bc,ab,ac,bc,共10种,其中均为矮茎的选取方式有ab,ac,bc共3种,因此选取的植株均为矮茎的概率是$\frac{3}{10}$.(12分)
点评 本小题主要考查学生对概率统计知识的理解,以及统计案例的相关知识,同时考查学生的数据处理能力.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
17.已知在△ABC中,∠ACB=90°,BC=3,AC=4,P是线段AB上的点,则P到AC,BC的距离的乘积的最大值为( )
| A. | 3 | B. | 2 | C. | $2\sqrt{3}$ | D. | 9 |
1.已知定义域为R的函数f(x)的图象经过点(1,1),且对任意实数x1<x2,都有$\frac{{f({x_1})-f({x_2})}}{{{x_1}-{x_2}}}>-2$,则不等式$f({log_2}|{3^x}-1|)<3-{log_{\sqrt{2}}}|{3^x}-1|$的解集为( )
| A. | (-∞,0)∪(0,1) | B. | (0,+∞) | C. | (-1,0)∪(0,3) | D. | (-∞,1) |
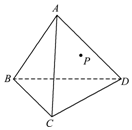 如图,有一个正三棱锥的零件,P是侧面ACD上的一点.过点P作一个与棱AB垂直的截面,怎样画法?并说明理由.
如图,有一个正三棱锥的零件,P是侧面ACD上的一点.过点P作一个与棱AB垂直的截面,怎样画法?并说明理由. 秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )
秦九昭是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九昭算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九昭算法求某多项式值的一个实例,若输入n,x的值分别为3,4,则输出y的值为( )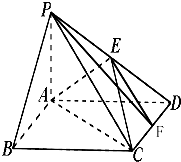 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点E为PD的中点,点F在棱DC上移动.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,PA=AD=1,AB=$\sqrt{3}$,点E为PD的中点,点F在棱DC上移动.