题目内容
已知P是△ABC所在平面内的点,且
+2
+3
=3
,
(1)求证:点P在直线AB上;
(2)求△PAC与△PBC的面积之比.
| PA |
| PB |
| PC |
| AC |
(1)求证:点P在直线AB上;
(2)求△PAC与△PBC的面积之比.
考点:向量在几何中的应用
专题:计算题,作图题,证明题,平面向量及应用
分析:(1)由
+2
+3
=3
经线性运算可化得2
+
=
,从而证明;
(2)如图,由2
+
=
可得
=
;从而可得S△PAC:S△PBC=
=
.
| PA |
| PB |
| PC |
| AC |
| PA |
| PB |
| 0 |
(2)如图,由2
| PA |
| PB |
| 0 |
| h1 |
| h2 |
| 1 |
| 2 |
| ||
|
| 1 |
| 2 |
解答:
 解:(1)证明:∵
解:(1)证明:∵
+2
+3
=3
,
∴
+2
+3
-3
=
;
∴
+2
+3
=
;
∴2
+
=
;
∴点P在直线AB上;
(2)∵2
+
=
,
∴
=
;
故S△PAC:S△PBC=
=
.
 解:(1)证明:∵
解:(1)证明:∵| PA |
| PB |
| PC |
| AC |
∴
| PA |
| PB |
| PC |
| AC |
| 0 |
∴
| PA |
| PB |
| PA |
| 0 |
∴2
| PA |
| PB |
| 0 |
∴点P在直线AB上;
(2)∵2
| PA |
| PB |
| 0 |
∴
| h1 |
| h2 |
| 1 |
| 2 |
故S△PAC:S△PBC=
| ||
|
| 1 |
| 2 |
点评:本题考查了向量的线性运算,同时考查了向量在几何中的应用,属于中档题.

练习册系列答案
相关题目
已知a、b、c都是实数,则“ac2>bc2”是“a>b”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
管理人员从一池塘内捞出30条鱼,做上标记后放回池塘.10天后,又从池塘内捞出50条鱼,其中有标记的有2条.根据以上数据可以估计该池塘内共有( ) 条鱼.
| A、250 | B、300 |
| C、500 | D、750 |
已知定点M(-1,0),N(1,0),P是椭圆
+
=1上动点,则
+
的最小值为( )
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| |PM| |
| 4 |
| |PN| |
| A、2 | ||
B、
| ||
| C、3 | ||
D、3+2
|
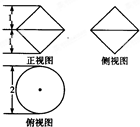 某几何体的三视图如图所示,则该几何体的体积为( )
某几何体的三视图如图所示,则该几何体的体积为( )A、
| ||
B、2
| ||
C、
| ||
D、
|
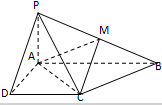 如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=