题目内容
已知f（x）=
，则f（
）的值为 ．
|
| 4 |
| 3 |
考点：绝对值不等式的解法
专题：三角函数的求值
分析：由题意可得f（
）=f（
）+1=f（-
）+2=cos（-
）+2，利用诱导公式计算求得结果．
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2π |
| 3 |
解答：
解：∵f（x）=
，
则f（
）=f（
）+1=f（-
）+2=cos（-
）+2=cos
+2=-
+2=
，
故答案为：
．
|
则f（
| 4 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
故答案为：
| 3 |
| 2 |
点评：本题主要考查利用函数的解析式求函数的值，诱导公式，体现了转化的数学思想，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
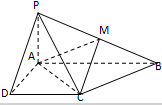如图所示，已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=
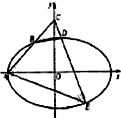已知B（-1，1）是椭圆