题目内容
已知数列{an}的各项均为正数,Sn表示数列{an}的前n项的和,且2Sn=a
+an.
(1)求数列{an}的通项;
(2)设bn=an•2 an,求{bn}的前n项和Tn.
2 n |
(1)求数列{an}的通项;
(2)设bn=an•2 an,求{bn}的前n项和Tn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)首先利用递推关系求出数列的通项公式,
(2)利用(1)的结论进一步利用乘公比错位相减法求数列的和.
(2)利用(1)的结论进一步利用乘公比错位相减法求数列的和.
解答:
解:(1)2S1=
+a1
∴a1=1,
当n≥2时,2an=2Sn-2Sn-1=
+an-
-an-1
又∵an>0,
∴an=an-1+1,
∴{an}是以1为首项,以1为公差的等差数列,
故:an=a1+(n-1)d
=n.
(2)由题意可设:Tn=1×21+2×22+3×23+…+n×2n,
2Tn=1×22+2×22+…+n×2 n+1,
则:Tn=(n-1)2n-1+2.
| a | 2 1 |
∴a1=1,
当n≥2时,2an=2Sn-2Sn-1=
| a | 2 n |
| a | 2 n-1 |
又∵an>0,
∴an=an-1+1,
∴{an}是以1为首项,以1为公差的等差数列,
故:an=a1+(n-1)d
=n.
(2)由题意可设:Tn=1×21+2×22+3×23+…+n×2n,
2Tn=1×22+2×22+…+n×2 n+1,
则:Tn=(n-1)2n-1+2.
点评:本题考查的知识要点:数列通项公式的求法,乘公比错位相减法的应用,属于基础题型.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
如图所示,在正方体ABCD-A1B1C1D1中,直线B1D1与平面BDC1的位置关系是( )
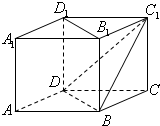

| A、平行 |
| B、垂直 |
| C、相交但不垂直 |
| D、直线B1D1在平面BDC1内 |
三个数a=30.4,b=0.43,c=log0.43大小关系为( )
| A、b<c<a |
| B、b<a<c |
| C、b<a<c |
| D、c<b<a |
已知a、b、c都是实数,则“ac2>bc2”是“a>b”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
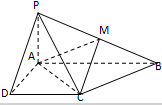 如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=