题目内容
函数f(x)=sinxcosx-
cos(π+x)cosx(x∈R).
(1)求f(x)的最小正周期;
(2)求f(x)的值域、单调区间.
| 3 |
(1)求f(x)的最小正周期;
(2)求f(x)的值域、单调区间.
考点:三角函数中的恒等变换应用
专题:三角函数的求值,三角函数的图像与性质
分析:(1)首先利用三角函数的恒等变换把函数的关系式变形成正弦型函数,进一步利用正弦型公式求出函数的最小正周期.
(2)利用整体思想求出函数的值域和单调区间.
(2)利用整体思想求出函数的值域和单调区间.
解答:
解:(1)f(x)=sinxcosx-
cos(π+x)cosx
=
sin2x+
•
=sin(2x+
)+
所以函数f(x)的正周期为:T=
=π.
(2)①x∈R
所以:-1≤sin(2x+
)≤1.
则:
-1≤f(x)≤1+
②令:-
+2kπ≤2x+
≤
+2kπ(k∈Z)
解得:-
+kπ≤x≤
+kπ
所以函数的单调增区间为:[-
+kπ,
+kπ](k∈Z).
令:
+2kπ≤2x+
≤
+2kπ(k∈Z)
解得:
+kπ≤x≤
+kπ
所以函数的单调递减区间为:[
+kπ,
+kπ](k∈Z).
| 3 |
=
| 1 |
| 2 |
| 3 |
| cos2x+1 |
| 2 |
=sin(2x+
| π |
| 3 |
| ||
| 2 |
所以函数f(x)的正周期为:T=
| 2π |
| 2 |
(2)①x∈R
所以:-1≤sin(2x+
| π |
| 3 |
则:
| ||
| 2 |
| ||
| 2 |
②令:-
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
解得:-
| 5π |
| 12 |
| π |
| 12 |
所以函数的单调增区间为:[-
| 5π |
| 12 |
| π |
| 12 |
令:
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
解得:
| π |
| 12 |
| 7π |
| 12 |
所以函数的单调递减区间为:[
| π |
| 12 |
| 7π |
| 12 |
点评:本题考查的知识要点:三角函数关系式的恒等变换,正弦型函数的周期的公式的应用,正弦型函数单调性的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
曲线f(x)=
在点(1,f(1))处切线的倾斜角为
,则实数a=( )
| x2+a |
| x+1 |
| 3π |
| 4 |
| A、1 | B、-1 | C、7 | D、-7 |
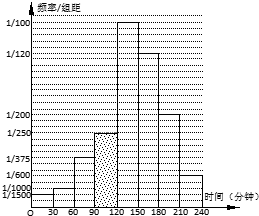 为了调查学生星期天晚上学习时间利用问题,某校从高二年级100名学生(其中走读生450名,住宿生550名)中,采用分层抽样的方法抽取n名学生进行问卷调查,根据问卷取得了这n名同学每天晚上学习时间(单位:分钟)的数据,按照以下区间分为八组
为了调查学生星期天晚上学习时间利用问题,某校从高二年级100名学生(其中走读生450名,住宿生550名)中,采用分层抽样的方法抽取n名学生进行问卷调查,根据问卷取得了这n名同学每天晚上学习时间(单位:分钟)的数据,按照以下区间分为八组