题目内容
已知sinα+sinβ+sinγ=0，cosα+cosβ+cosγ=0，则cos（α-β）的值是（ ）
| A、1 | ||
| B、-2 | ||
C、
| ||
D、-
|
考点：两角和与差的余弦函数
专题：三角函数的求值
分析：由条件利用sin2γ+cos2γ=1消掉γ即可得到结论．
解答：
解：由sinα+sinβ+sinγ=0，cosα+cosβ+cosγ=0，
得sinα+sinβ=-sinγ，cosα+cosβ=-cosγ，
平方相加得sin2γ+cos2γ=（sinα+sinβ）2+（cosα+cosβ）2=2=2+2sinαsinβ+2cosαcosβ=2+2cos（α-β）=1，
即cos（α-β）=-
，
故选：D
得sinα+sinβ=-sinγ，cosα+cosβ=-cosγ，
平方相加得sin2γ+cos2γ=（sinα+sinβ）2+（cosα+cosβ）2=2=2+2sinαsinβ+2cosαcosβ=2+2cos（α-β）=1，
即cos（α-β）=-
| 1 |
| 2 |
故选：D
点评：本题主要考查三角函数值的化简和求解，利用平方法，利用两角和差的余弦公式是解决本题的关键．
练习册系列答案
相关题目
如图1是某学习小组学生数学考试成绩的茎叶图，1号到16号同学的成绩依次为A1，A2，…，A16，图2是茎叶图中成绩在一定范围内的学生人数的算法流程图，那么该算法流程图输出的结果是（ ）
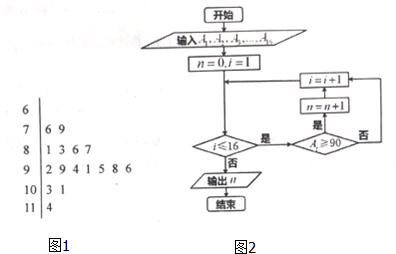
| A、6 | B、10 | C、91 | D、92 |
若函数y=f（2x+1）的定义域为[-1，2]，则g（x）=f（x）+f（-x）的定义域是（ ）
| A、[-1，1] |
| B、[-5，5] |
| C、[-1，5] |
| D、[-5，1] |
设扇形的周长为8cm，面积为4cm2，则扇形的圆心角是（ ）rad．
| A、1 | B、2 | C、π | D、1或2 |
m=0是方程x2+y2-4x+2y+m=0表示圆的（ ）条件．
| A、充分不必要 |
| B、必要不充分 |
| C、充要 |
| D、既不充分也不必要 |
不等式x2-x-6＜0解集为（ ）
| A、{x|-2＜x＜3} |
| B、{x|-3＜x＜2} |
| C、{x|x＜-3或x＞2} |
| D、{x|-1＜x＜6} |
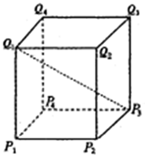若正方体P1P2P3P4-Q1Q2Q3Q4的棱长为1，集合M={x|x=