题目内容
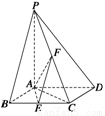
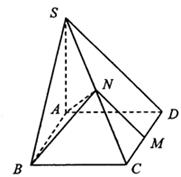
如图所示，已知四棱锥S—ABCD的底面ABCD是矩形，M、N分别是CD、SC的中点，SA⊥底面ABCD，SA=AD=1，AB=
.
（1）求证：MN⊥平面ABN；
（2）求二面角A—BN—C的余弦值.
|
解析:
以A点为原点，AB为x轴，AD为y轴，
AD为z轴的空间直角坐标系，
则依题意可知相关各点的坐标分别是
A（0，0，0），B（
，0，0），C（，1，0），D（0，1，0），S（0，0，1）
∴MN⊥平面ABN.
（2）设平面NBC的法向量
且又易知
令a=1，则
显然，
就是平面ABN的法向量.
练习册系列答案
相关题目
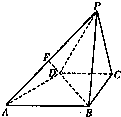如图所示，已知四棱锥P-ABCD的底面是直角梯形，∠ABC=∠BCD=90°，AB=BC=PB=PC=2，CD=1，侧面PBC⊥底面ABCD，点F在线段AP上，且满足
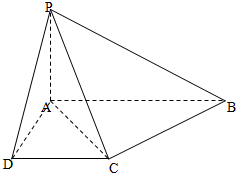如图所示，已知四棱锥P-ABCD的底面为直角梯形，AB∥DC，∠DAB=90°，PA⊥底面ABCD，且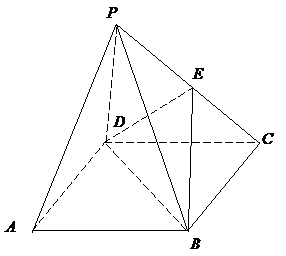
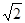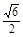中，底面
为正方形，侧面
为正三角形，且平面
底面
为
中点，求证：
平面
； （２）平面
平面
．
.
,