题目内容
9.已知函数f(x)=$\frac{{2}^{x}+b}{{2}^{x}+a}$(a、b为常数),且f(1)=$\frac{1}{3}$,f(0)=0.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)判断函数f(x)在定义域上的奇偶性,并证明.
分析 (Ⅰ)由已知中f(1)=$\frac{1}{3}$,f(0)=0.构造方程组,可得a,b值,进而得到函数f(x)的解析式;
(Ⅱ)函数f(x)为奇函数.利用奇偶性可证得结论.
解答 解:(Ⅰ)由已知可得f(1)=$\frac{2+b}{2+a}$=$\frac{1}{3}$,f(0)=$\frac{1+b}{1+a}$=0,….(3分)
解得a=1,b=-1,
所以f(x)=$\frac{{2}^{x}-1}{{2}^{x}+1}$;…(5分)
(Ⅱ) 函数f(x)为奇函数.
证明如下:f(x)的定义域为R,….(6分)
∵f(-x)=$\frac{{2}^{-x}-1}{{2}^{-x}+1}$=$\frac{{1-2}^{x}}{{2}^{x}+1}$=-f(x),….(9分)
∴函数f(x)为奇函数;…(10分)
点评 本题考查的知识点是函数解析式的求法,函数的奇偶性,难度中档.

练习册系列答案
相关题目
14.要得到函数y=sinx的图象,只需将函数$y=sin(x-\frac{π}{3})$的图象( )
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
17.在等腰直角△ABC中,∠ABC=90°,AB=BC=2,M,N(不与A,C重合)为AC边上的两个动点,且满足|$\overrightarrow{MN}$|=$\sqrt{2}$,则$\overrightarrow{BM}$•$\overrightarrow{BN}$的取值范围为( )
| A. | [$\frac{3}{2}$,2] | B. | ($\frac{3}{2}$,2) | C. | [$\frac{3}{2}$,2) | D. | [$\frac{3}{2}$,+∞) |
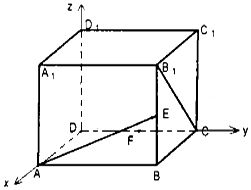 在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点,
在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点,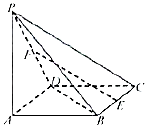 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA=AB=2,$PB=2\sqrt{2}$,$PC=2\sqrt{3}$,E,F分别为BC,PD的中点.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA=AB=2,$PB=2\sqrt{2}$,$PC=2\sqrt{3}$,E,F分别为BC,PD的中点.