题目内容
19.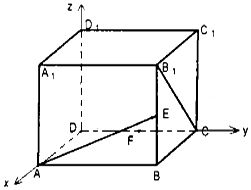 在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点,
在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点,(1)求证:D1F⊥AE;
(2)求直线EF与CB1所成角的余弦值.
分析 (1)依题意分别求得A,E,D1和F的坐标,求出$\overrightarrow{AE}$,$\overrightarrow{{D}_{1}F}$,二者相乘等于0即可证明出AE⊥D1F进而根据线面垂直的性质证明出D1F⊥AD,最后根据线面垂直的判定定理证明出D1F⊥平面ADE.
(2)分别求得$\overrightarrow{EF}$=(2,1,1),$\overrightarrow{C{B}_{1}}$=(1,0,1),利用向量的夹角公式求得异面直线所成角的余弦值.
解答 (1)证明:依题意知D(0,0,0),A(2,0,0),F(0,1,0),E(2,2,1),A1(2,0,2),D1(0,0,2),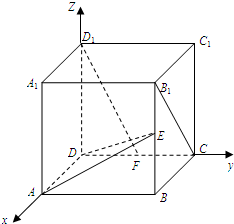
$\overrightarrow{AE}$=(0,0,1),$\overrightarrow{{D}_{1}F}$=(0,1,-2),
∴$\overrightarrow{AE}$•$\overrightarrow{{D}_{1}F}$=0,
∴AE⊥D1F;
∵AD⊥平面CDD1C1,D1F?平面CDD1C1,
∴D1F⊥AD,
∵AE?平面ADE,AD?平面ADE,AE∩AD=A,
∴D1F⊥平面ADE.
(2)解:依题意可知B1(1,1,1),C(0,1,0),F(0,1,0),E(2,2,1),
∴$\overrightarrow{EF}$=(2,1,1),$\overrightarrow{C{B}_{1}}$=(1,0,1),
∴cos<$\overrightarrow{EF}$,$\overrightarrow{C{B}_{1}}$>=$\frac{\sqrt{3}}{2}$,
∴异面直线EF和CB1所成的角余弦值为$\frac{\sqrt{3}}{2}$.
点评 本题主要考查了线面垂直和空间向量的应用.考查了学生综合分析和运算能力.

| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{2}$ | D. | $\frac{3π}{4}$ |