题目内容
7.设函数y=f(x)是定义在上(0,+∞)的减函数,并且满足f(xy)=f(x)+f(y),$f(\frac{1}{3})=\frac{1}{2}$.(1)求f(1);
(2)若存在实数m,使得f(m)=1,求m的值;
(3)若f(x-2)>1+f(x),求x的取值范围.
分析 (1)利用赋值法令x=y=1,代入求解即可.
(2)根据抽象函数的关系进行求解即可.
(3)根据函数单调性以及抽象函数的关系解不等式即可.
解答 解:(1)令x=y=1,则f(1)=f(1)+f(1),
∴f(1)=0.
(2)∵f($\frac{1}{3}$)=$\frac{1}{2}$,
∴f($\frac{1}{9}$)=f($\frac{1}{3}$×$\frac{1}{3}$)=f($\frac{1}{3}$)+f($\frac{1}{3}$)=$\frac{1}{2}$+$\frac{1}{2}$=1,
∴m=$\frac{1}{9}$;
(3))∵f(x-2)>1+f(x),
∴f(x-2)>f($\frac{1}{9}$)+f(x)=f($\frac{1}{9}$x),
∵函数y=f(x)是定义在(0,+∞)上的减函数,
∴$\left\{\begin{array}{l}{x-2>0}\\{x>0}\\{x-2<\frac{1}{9}x}\end{array}\right.$即$\left\{\begin{array}{l}{x>2}\\{x>0}\\{x<\frac{9}{4}}\end{array}\right.$,得2<x<$\frac{9}{4}$,
∴x的取值范围2<x<$\frac{9}{4}$.
点评 本题主要考查函数的单调性及运用,考查解决抽象函数的常用方法:赋值法,考查基本的运算能力.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
18.若函数f(x)唯一的零点同时在(1,1.5),(1.25,1.5),(1.375,1.5),(1.4375,1.5)内,则该零点(精确度为0.01)的一个近似值约为( )
| A. | 1.02 | B. | 1.27 | C. | 1.39 | D. | 1.45 |
19.直线ax-2by+1=0(a>0,b>0)平分圆x2+y2+4x-2y-1=0的面积,则$\frac{1}{a}$+$\frac{2}{b}$的最小值为( )
| A. | 3+2$\sqrt{2}$ | B. | 4+2$\sqrt{3}$ | C. | 6+4$\sqrt{2}$ | D. | 8$\sqrt{3}$ |
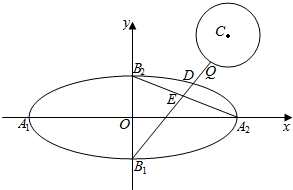 如图,已知椭圆$\frac{{x}^{2}}{2}$+y2=1的四个顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,若圆C:(x-3)2+(y-3)2=r2(0<r<3)上有且只有一个点P满足$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\sqrt{5}$.
如图,已知椭圆$\frac{{x}^{2}}{2}$+y2=1的四个顶点分别为A1,A2,B1,B2,左右焦点分别为F1,F2,若圆C:(x-3)2+(y-3)2=r2(0<r<3)上有且只有一个点P满足$\frac{|P{F}_{1}|}{|P{F}_{2}|}$=$\sqrt{5}$.