题目内容
【题目】在平面直角坐标系![]() 中,
中,![]() 为抛物线
为抛物线![]() 上不同的两点,且
上不同的两点,且![]() ,点
,点![]()
![]() 且
且![]() 于点
于点![]() .
.
(1)求![]() 的值;
的值;
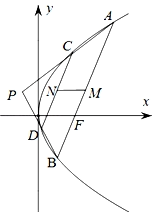
(2)过![]() 轴上一点
轴上一点 ![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,
两点,![]() 在
在![]() 的准线上的射影分别为
的准线上的射影分别为![]() ,
,![]() 为
为![]() 的焦点,若
的焦点,若![]() ,求
,求![]() 中点
中点![]() 的轨迹方程.
的轨迹方程.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由点![]() 且
且![]() 于点
于点![]() ,可求得直线AB的方程,联立直线方程与抛物线方程由韦达定理可表示
,可求得直线AB的方程,联立直线方程与抛物线方程由韦达定理可表示![]() ,进而表示
,进而表示![]() ,再由
,再由![]() ,得
,得![]() 构建方程,解得p值;
构建方程,解得p值;
(2)分别表示![]() 与
与![]() ,由已知
,由已知![]() 构建方程,解得t的值,设
构建方程,解得t的值,设![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,当
,当![]() 与
与![]() 轴不垂直时,由
轴不垂直时,由![]() 构建等式,整理得中点轨迹方程;当
构建等式,整理得中点轨迹方程;当![]() 与
与![]() 轴垂直时,
轴垂直时,![]() 与
与![]() 重合,综上可得答案.
重合,综上可得答案.
(1)由![]() 及
及![]() ,得直线
,得直线![]() 的斜率
的斜率![]() ,
,
则![]() 的方程为
的方程为![]() ,即
,即![]() ,
,
设![]() ,
,![]() ,
,
联立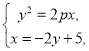 消去
消去![]() 得
得![]() ,
,![]() ,
,
由韦达定理,得![]() ,于是
,于是![]() ,
,
由![]() ,得
,得![]() ,即
,即![]() ,则
,则![]() ,
,
解得![]() .
.
(2)由(1)得抛物线的焦点![]() ,设
,设![]() 的准线与
的准线与![]() 轴的交点为
轴的交点为![]() ,
,
则![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,且
,且![]() ,得
,得![]() .
.
设![]() 的中点
的中点![]() 的坐标为
的坐标为![]() ,
,
则当![]() 与
与![]() 轴不垂直时,由
轴不垂直时,由![]() ,
,
可得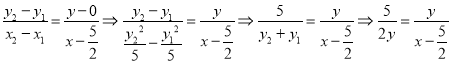 ,
,
![]() ;
;
当![]() 与
与![]() 轴垂直时,
轴垂直时,![]() 与
与![]() 重合,
重合,
所以![]() 的中点的轨迹方程为
的中点的轨迹方程为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目