Question

【题目】在△ABC中，a，c，________.（补充条件）

（1）求△ABC的面积；

（2）求sin（A+B）.

从①b＝4，②cosB，③sinA这三个条件中任选一个，补充在上面问题中并作答.

Answer 1

【答案】详见解析

【解析】

选择①（1）先由余弦定理求得cosC，进而求得sinC，由此求得面积；

（2）sin（A+B）＝sinC，直接可以得出答案；

选择②（1）利用平方关系求得sinB，进而求得面积；

（2）先由余弦定理求得b，再由正弦定理求得sinC，进而得解；

选择③（1）先由平方关系求得cosA，再由余弦定理求得b，进而求得面积；

（2）由正弦定理可得，由此即可得解.

选择①

（1）在△ABC中，因为，，b＝4，

由余弦定理得，

因为C∈（0，π），所以，

所以.

（2）在△ABC中，A+B＝π﹣C.

所以.

选择②

（1）因为，B∈（0，π），所以，

因为，，所以.

（2）因为，，，

由b2＝a2+c2﹣2accosB，得，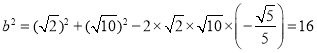

解得b＝4，

由，解得，

在△ABC中，A+B＝π﹣C，.

选择③

依题意，A为锐角，由，得，

在△ABC中，因为，，，

由余弦定理a2＝b2+c2﹣2bccosA，得，

解得b＝2或b＝4，

（1）当b＝2时，.

当b＝4时，.

（2）由，，，，得，

在△ABC中，A+B＝π﹣C，.