题目内容
【题目】对有![]() 个元素的总体
个元素的总体![]() 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体![]() 和
和![]() (
(![]() 是给定的正整数,且
是给定的正整数,且![]() ),再从每个子总体中各随机抽取2个元素组成样本.用
),再从每个子总体中各随机抽取2个元素组成样本.用![]() 表示元素
表示元素![]() 和
和![]() 同时出现在样本中的概率.
同时出现在样本中的概率.
(1)求![]() 的表达式(用
的表达式(用![]() ,
,![]() 表示);
表示);
(2)求所有![]() 的和.
的和.
【答案】(1)![]() ;(2)6
;(2)6
【解析】
(1)根据组合数的公式,以及古典概型的概率计算公式和相互独立事件的概率计算公式,即可求解;
(2)当![]() 都在
都在![]() 中时求得
中时求得![]() 的和为1,当
的和为1,当![]() 同时在
同时在![]() 中时,求得
中时,求得![]() 的和为1,当
的和为1,当![]() 在
在![]() 中,
中,![]() 在
在![]() 中时得到
中时得到![]() 的和为4,即可求解.
的和为4,即可求解.
(1)由题意,从![]() 和
和![]() 个式子中随机抽取2个,分别有
个式子中随机抽取2个,分别有![]() 和
和![]() 个基本事件,
个基本事件,
所以![]() 的表达式为
的表达式为![]() .
.
(2)当![]() 都在
都在![]() 中时,可得
中时,可得![]() ,
,
而从![]() 中选两个数的不同方法数为
中选两个数的不同方法数为![]() ,则
,则![]() 的和为1;
的和为1;
当![]() 同时在
同时在![]() 中时,同理可得
中时,同理可得![]() 的和为1;
的和为1;
当![]() 在
在![]() 中,
中,![]() 在
在![]() 中时,
中时,![]() ,
,
而从![]() 中选取一个数,从
中选取一个数,从![]() 中选一个数的不同方法数为
中选一个数的不同方法数为![]() ,
,
则![]() 的和为4,所以所有
的和为4,所以所有![]() 的和为
的和为![]() .
.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案【题目】随着运动app和手环的普及和应用,在朋友圈、运动圈中出现了每天1万步的健身打卡现象,“日行一万步,健康一辈子”的观念广泛流传.“健步达人”小王某天统计了他朋友圈中所有好友(共500人)的走路步数,并整理成下表:
分组(单位:千步) |
|
|
|
|
|
|
|
|
频数 | 60 | 240 | 100 | 60 | 20 | 18 | 0 | 2 |
(1)请估算这一天小王朋友圈中好友走路步数的平均数(同一组中数据以这组数据所在区间中点值作代表);
(2)若用![]() 表示事件“走路步数低于平均步数”,试估计事件
表示事件“走路步数低于平均步数”,试估计事件![]() 发生的概率;
发生的概率;
(3)若称每天走路不少于8千步的人为“健步达人”,小王朋友圈中岁数在40岁以上的中老年人共有300人,其中健步达人恰有150人,请填写下面![]() 列联表.根据列联表判断,有多大把握认为,健步达人与年龄有关?
列联表.根据列联表判断,有多大把握认为,健步达人与年龄有关?
健步达人 | 非健步达人 | 合计 | |
40岁以上 | |||
不超过40岁 | |||
合计 |
附: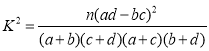 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
【题目】某省即将实行新高考,不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响,对该校2018级的1000名学生进行调查,收集到相关数据如下:
(1)根据以上提供的信息,完成![]() 列联表,并完善等高条形图;
列联表,并完善等高条形图;
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
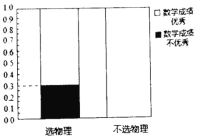
(2)能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关?
附: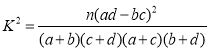
临界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |