题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)若![]() 在定义域内是增函数,且存在不相等的正实数
在定义域内是增函数,且存在不相等的正实数![]() ,使得
,使得![]() ,证明:
,证明:![]() .
.
【答案】(1)当![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减;
上递减;
当![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
当![]() 时,
时,![]() 在
在![]() 上递增;
上递增;
当![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
(2)证明见解析
【解析】
(1)对![]() 求导,分
求导,分![]() ,
,![]() ,
,![]() 进行讨论,可得
进行讨论,可得![]() 的单调性;
的单调性;
(2)![]() 在定义域内是是增函数,由(1)可知
在定义域内是是增函数,由(1)可知![]() ,
,![]() ,设
,设![]() ,可得
,可得![]() ,则
,则![]() ,设
,设![]() ,对
,对![]() 求导,利用其单调性可证明
求导,利用其单调性可证明![]() .
.
解:![]() 的定义域为
的定义域为![]() ,
,
因为![]() ,
,
所以![]() ,
,
当![]() 时,令
时,令 ,得
,得![]() ,令
,令 ,得
,得![]() ;
;
当![]() 时,则
时,则![]() ,令
,令 ,得
,得![]() ,或
,或![]() ,
,
令 ,得
,得![]() ;
;
当![]() 时,
时,![]() ,
,
当![]() 时,则
时,则![]() ,令
,令 ,得
,得![]() ;
;
综上所述,当![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减;
上递减;
当![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
当![]() 时,
时,![]() 在
在![]() 上递增;
上递增;
当![]() 时,
时,![]() 在
在![]() 上递增,在
上递增,在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
(2)![]() 在定义域内是是增函数,由(1)可知
在定义域内是是增函数,由(1)可知![]() ,
,
此时![]() ,设
,设![]() ,
,
又因为![]() ,则
,则![]() ,
,
设![]() ,则
,则
 对于任意
对于任意![]() 成立,
成立,
所以![]() 在
在![]() 上是增函数,
上是增函数,
所以对于![]() ,有
,有![]() ,
,
即![]() ,有
,有![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即![]() ,又
,又![]() 在
在![]() 递增,
递增,
所以![]() ,即
,即![]() .
.

【题目】随着运动app和手环的普及和应用,在朋友圈、运动圈中出现了每天1万步的健身打卡现象,“日行一万步,健康一辈子”的观念广泛流传.“健步达人”小王某天统计了他朋友圈中所有好友(共500人)的走路步数,并整理成下表:
分组(单位:千步) |
|
|
|
|
|
|
|
|
频数 | 60 | 240 | 100 | 60 | 20 | 18 | 0 | 2 |
(1)请估算这一天小王朋友圈中好友走路步数的平均数(同一组中数据以这组数据所在区间中点值作代表);
(2)若用![]() 表示事件“走路步数低于平均步数”,试估计事件
表示事件“走路步数低于平均步数”,试估计事件![]() 发生的概率;
发生的概率;
(3)若称每天走路不少于8千步的人为“健步达人”,小王朋友圈中岁数在40岁以上的中老年人共有300人,其中健步达人恰有150人,请填写下面![]() 列联表.根据列联表判断,有多大把握认为,健步达人与年龄有关?
列联表.根据列联表判断,有多大把握认为,健步达人与年龄有关?
健步达人 | 非健步达人 | 合计 | |
40岁以上 | |||
不超过40岁 | |||
合计 |
附: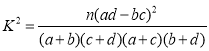 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |