题目内容
10.将函数$y=2sin(2x+\frac{π}{6})$的图象向左平移$\frac{1}{4}$个周期后,所得图象对应的函数为( )| A. | $y=2sin(2x+\frac{2π}{3})$ | B. | $y=2sin(2x+\frac{5π}{12})$ | C. | $y=2sin(2x-\frac{π}{3})$ | D. | $y=2sin(2x-\frac{π}{12})$ |
分析 由已知函数解析式求得函数周期,再结合三角函数的图象平移得答案.
解答 解:函数$y=2sin(2x+\frac{π}{6})$的周期T=$\frac{2π}{2}=π$,
将函数$y=2sin(2x+\frac{π}{6})$的图象向左平移$\frac{1}{4}$个周期,即向左平移$\frac{π}{4}$个单位,
∴平移后所得图象对应的函数为y=$2sin[2(x+\frac{π}{4})+\frac{π}{6}]$=$2sin(2x+\frac{2π}{3})$.
故选:A.
点评 本题考查三角函数的图象和性质,考查三角函数的图象平移,是基础题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
1.设集合A={x|x<2},B={y|y=2x-1,x∈A},则A∩B=( )
| A. | (-∞,3) | B. | [2,3) | C. | (-∞,2) | D. | (-1,2) |
5.已知函数$f(x)=\left\{\begin{array}{l}\sqrt{x}+3,x≥0\\ ax+b,x<0\end{array}\right.$满足条件:对于?x1∈R,且x1≠0,?唯一的x2∈R且x1≠x2,使得f(x1)=f(x2).当f(2a)=f(3b)成立时,则实数a+b=( )
| A. | $\frac{{\sqrt{6}}}{2}$ | B. | $-\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{6}}}{2}$+3 | D. | $-\frac{{\sqrt{6}}}{2}$+3 |
15.已知f(x),g(x)都是定义在R上的函数,g(x)≠0,f(x)g′(x)>f′(x)g(x),f(x)=ax•g(x)(a>0,a≠1),$\frac{f(1)}{g(1)}+\frac{f(-1)}{g(-1)}=\frac{5}{2}$,在有穷数列$\{\frac{f(n)}{g(n)}\}$(n=1,2…10)中,任意取正整数k(1≤k≤10),则前k项和大于$\frac{15}{16}$的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
2.一个篮球运动员投篮一次得3分的概率为a,得2分的概率为b,不得分的概率为c(a,b,c∈(0,1)),已知他投篮一次得分的数学期望为2,则$\frac{2}{a}+\frac{1}{3b}$的最小值为( )
| A. | $\frac{32}{3}$ | B. | $\frac{28}{3}$ | C. | $\frac{16}{3}$ | D. | 4 |
19.已知某三棱锥的三视图如图所示,则该三棱锥外接球的表面积是( )
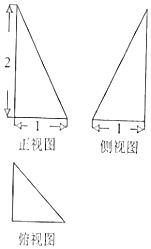

| A. | $\sqrt{6}π$ | B. | 6π | C. | 24π | D. | 36π |